Keywords

Computational simulation; Analogy process; Artificial intelligence; Semi analogy

Introduction

As Gentner and Forbus (2011) stated, modeling the analogy process is composed of several sub-processes, among which the following are fundamental.

•Retrieval: Given a domain, it is identified as an analog one and retrieving it through long-term memory.

•Mapping: Given the two mentioned domains, a list of possible correspondences between them is established.

•Abstraction (or generalization): It is schematized the result of this correspondence so that it can later be used by the system as a structural similarity which can further be applied to some other domains.

•Re-representation: Improving mapping by modifying partial matching.

As an instance of analogical reasoning simulation in the realm of artificial intelligence, a case-based reasoning example can be examined. This model is intended to solve a given problem by looking for another similar one. This process works based on a previously built collection of pairs (problem, solution) from which a pair containing a similar problem to the actual one is taken as a base problem. Then, if the solution (B, A) is known and C is like A, it can be expected to have D as a solution of C. This is the well-known proportional analogy schema that states that D is to C like B is to A [1].

Overall, regarding Problem C, (B, A) is taken as the most familiar pair the process can gather from the collection. Rhetorically, (B, A) is called forum, while the pair (D, C) is the theme. Since the pair (B, A) is already known then, were C closely enough to A, an analogical transfer to Pair (D, C) would be stated. Given this situation, it can be claimed that C is related to D as A is related to B. Hence, an analogy is a transfer of relational structure from the forum to the theme. In the realm of artificial intelligence, the most familiar domain which is the forum becomes the source domain; while the theme becomes the target domain. As it is understood by Husserl’s phenomenology, the world appears to consciousness by way of a process of constitution, which leads to the formation of noema. As it is claimed here, objectivities constitution is based on the process of analogy, particularly on the analogical property of mediation. On one side, from an analogical perspective, objectivities are constituted through mediation using contrast, memory, wholes-parts, meanings, and other objectivities. On the other hand, the whole-parts relationship, as Husserl shows in the third of his Logical Investigations [1] is the formal frame to account for distinguishing between independent and not-independent parts. These differences can be viewed as the possibility or impossibility of such objects to be separable from each other. The mediation property of analogy and the analogy itself can be regarded in terms of the formal frame of Husserl’s theory of wholes and parts [2].

Analogical mediation means that entailment between a given pair of objects (A, B) and another pair (C, D) regards some kind of similarity between them. In this sense, A entails B the way C entails D, and this way is just mediation. In other words, A entails B using entailment between C and D. Now, regarding the concept of foundation, we can say that known pair (C, D) grounds the pair (A, B). In this sense, what is mediated is caught and made explicit through what is immediate and motivates the analogical relation. Besides, what is immediate and outstanding from a given background comes up as what is already known or more or less familiar. By using Husserl’s terminology, while the analogical configuration A:B :: C:D constitutes a whole unity, the relation A:B constitutes a moment of that whole, i.e., an inseparable and dependent part of the analogical unit. The same can be said about the relation C:D. Rules governing mediation, dependency, and foundation apply to whole-parts relationships.

Phenomenological Principle of Ordered Mediation

According to the last, what is mediated presupposes what is immediate. As Husserl claims, a particular understanding of the mediate part presupposes the immediate part being particularly shown up (Husserl 1984, (271)). This does not mean that the immediate must be understood before the mediate, but rather that the mediate must be understood in so far as it needs to be supplemented by the immediate. Let us illustrate this by thinking of a line in which, for example, every singular part as a partial segment of the line presupposes that a linear space between its edge and the whole line’s edge is covered. As immediate parts, the partial segments lay down distances and directions, but what is caught as a consciousness object is the whole line. In summary, the mediated unit is caught as a whole object, and the immediate is simply outstanding.

As Peter Simons states, one of the main differences between Husserl’s whole-parts theory and others is that Husserl distinguishes independent parts and not independent parts (Smith, Parts and Moments Studies in Logic and Formal Ontology 1982, 215). There are two kinds of parts: moments (Momente) and fragments or pieces (Stücke). Moments are relatively dependent parts that are abstract, and the relatively independent parts are fragments (pieces). A fragment of a whole, although independent to that whole, is not absolutely (necessarily) so, since it could well be dependent on some other whole. Then, as it is stated in the third Logical Investigation, while a relatively dependent object is also absolutely dependent, a relatively independent object could be absolutely dependent (Husserl 1984, 269) [3]. 

The Concept of Foundation and Derived Theorems

Husserl uses the concept of foundation to display all possible dependency relations, for which he establishes the following definition:

If it is said that some A cannot exist as it is unless it is in a more comprehensive unity that connects it to an M, we can say that such an A requires to be grounded on that M. That is, such an A must be supplemented by an M.

The following propositions [2] are set by Husserl based on the notion of foundation.

Proposition 1

If some A needs to be grounded on some M, then every totality that contains an A, but not an M as a part of it, requires to be grounded similarly.

Although Husserl takes this proposition as an axiom, Fine (Smith y Smith 1995, 466) states the following axiom as grounding P1.

A1. (xFy ∧ x ≤ x⁺ ∧ ¬ (y ≤ x⁺)) → x⁺Fy

Where the term x⁺ represents some totality containing x

Contribution to Analogy (1)

If object A is founded on object M, then every totality containing A is also founded on M whenever M is not contained in that totality. As it can be seen from the proposition, the core of the analog unit is the existence of a mediated foundation. M founds both A and the totality that contains it, M being outside that totality. Or, the totality mediately is founded through A in M. According to axiom (A1), these foundations can be symbolized by making x=A, y=M [4].

To illustrate proposition (P1), it can be stated a “semi-analogical[3]” relation like boat:water :: boat fleet: water

This example shows foundation as function, i.e., boat functions by sailoring on water (lake, sea, river). Besides, the necessity is a kind of foundation. There are different kinds of foundation inclusion, function, component, ownership, feature, finality, etc. concerning nature’s object. From this perspective, Casari regards something that is founded as having need of, so boat needs (∂(x))) water.

For the formulation of the second proposition, the definitions (Smith and Smith 1995, 467) of the dependent part (DP), independent whole (unit) (IW), and relative dependent part (DPz) are required:

D1. DP(x) ≝ ∃ x(xFy)

D2. IW(x) ≝ ¬ DP(x)

D3. DP_z(x) ≝ (∃y ≤ z) (xFy)

Proposition 2

A totality that includes a non-independent 'moment', without including, as a part, the supplement that that moment demands, is likewise non-independent, and it is also non-independent to any higher independent totality in which that dependent moment is contained.

P2. (x ≤ x⁺∧ xFy ∧ ¬ y ≤ x⁺) → DP(x⁺) ∧ ∀ z (x ≤ z ∧ x⁺ ≤ z ∧ IW(z) → DP_z(x⁺))

According to (P2), Husserl considers a totality (X’) that includes a non-independent moment (X), and X does not include the supplement (Y) which X demands and is contained in a higher totality. To illustrate this, it can be stated:

P2. (x ≤ x⁺∧ xFy ∧ ¬ y ≤ x⁺)

X’: String sound
X: Guitar sound
Y: Guitar
Z: String musical instrument

The analog unit that can be formulated with these terms based on proposition 2 would be: X: X’:: Y: Z

To formulate the third proposition, the independent part (IP) notion is required:

D4. xlPy ≝ x ≤ y ∧ ¬ (∃ y′ ≤ y) (xFy′)

That is, the independent parts of a whole are parts that are not founded on any part of the whole.

Proposition 3

If W is an independent part of F, then every independent part w of W is also an independent part of F.

P3. xlPy ∧ yIPz → xIPz

Contribution to Analogy (3)

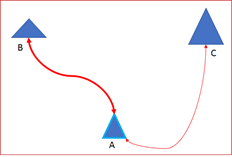
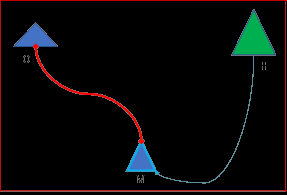
Regarding analogy, proposition 3 shows that if B is an independent part of A, and A is an independent part of C, then B is also an independent part of C. As it can be seen from Figure 1, A is the middle term and, regarding the whole/parts theory, it is the triangle “A”. Besides, and regarding passive syntheses (of homogeneity and heterogeneity) [4]the mediating element is the very link that fuses the triangles “A” and “B” at a distance due to their affinity. This very link between the two triangles allows a similar link to be established between the triangles “A” and “C”, which are also kindred to each other.

Just as the independent parts have been considered, the dependent parts can be understood before the next proposition according to the following definition.

D5. xDPy ≝ x ≤ y ∧ (∃ z ≤ y) (xFz)

Proposition 4

If C is a non-independent part of a totality W, it is also a non-independent part of any other totality W is a part of.

P4. xDPy ∧ y ≤ z → xDPz

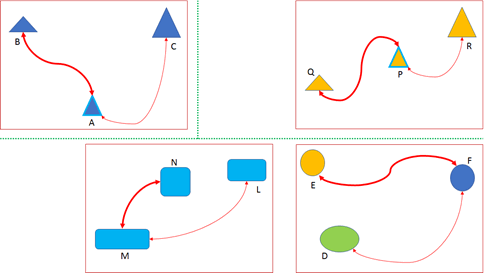
As it has been seen from proposition (P3), the notion of independence of parts is based on the idea of separability. How much two independent objects are separated is not important. That is, the distance measure is not relevant, so the magnitude of the bond that links the triangles is not important, but only the separation. Figure 2 shows analogical structures. Now, while proposition 3 regards independence, proposition 4 regards not-independence instead. From D5 it can be seen that dependence between parts is based on another part, i.e., a mediated one. 

Links highlighted (as thick ties) are similar to each other and, as it has been said, they are important insofar as they are motivators to configure analogical structures corresponding to the one of Figure 1. According to this, for example, pairs PQ and PR are correspondingly analog to pairs AB and AC. And analogously, similar structures can be expressed between the pairs MN and ML and between FD and FE. The role of element A consists of being a trigger to generate, already actively, any of the other three analogous situations. Then, any of the situations represented can function as a "family" structure to generate any other structurally similar situation by analogy. The situations illustrated in Figure 2 can be represented as in (Figure 3). The objects P, M, and F have the mediating function in their corresponding situations. That function is analogous to that of object A [5].

The situation of Figure 1, the original situation is what enables learning, which, in this case, is the configuration of objects as wholes. The uniqueness of each configuration is based on a structure that is apprehensible by two criteria: one of reason and the other of motivation. On the one hand, the criterion of the reason is based on the logical structure that supports the parity of the links. This structure is represented topologically in the examples seen. On the other hand, the motivation criterion is based on the mediating nature of the bridging element that synthesizes the homogeneity of the pairs. The former is established in the active sphere of the cognitive agent - such as a human being. The second is established as a reflection also active of a synthesis that is generated in the passive sphere. Both criteria converge in a constitution of objects with meaning: The objects are what they mean for the cognitive agent. While the original situation exists and passively appears to the cognitive agent, the structures analogous to it are actively found by him, or, possibly, passively.

Indeed, having learned from a situation means being able to recognize any future analogous situation as an instance of the same object, of the same configuration, like the one represented in Figure 1. Husserl describes objective existence as a unifying synthesis of multiple grasps of different aspects of the same thing. The same object now appears in one way, now in another, in other perspectives, and these perspectives point to others so that the object is more and more determined, more closely defined, and yet never definitively determined, but always determinable (Husserl 2001, 108). In this sense, memory is rather a capacity to reproduce, to revive what has been retained.

Regarding the analogy process, what is learned is the material retained and ready to form new learning; recoverable (retrieval) to be "processed", put into correspondence (mapping) with what is currently focused. The result of these two phases, the fused noematic material will be, after its schematization (abstraction) and its conformation as a noematic unit (re-representation), new hyletic, learned, and recursive matter. Presumably, such a procedure would be effective if we can determine a starting point: That of the original hyletic matter. As established in Hernández-Quiroz and Morado, "HILBERT, TURING AND THE NOTION OF EFFECTIVE PROCEDURE", as long as this procedure could be defined in terms of primitive-recursive functions, we would have a decidable set of functions, that is, an effective procedure whose evaluation would take a finite number of steps (Hernández-Quiroz y Morado 2006, 7). The finitude in the number of steps is regulated by the retrieval and mapping threads.

The elements of Figure 3 represent M: Mammal, O: Oviparous, and H: Human. The protagonist of this situation is the separation between M and O. This stands out given the fact that “All H is M”. Although the syllogistic conclusion is determined (analytically) by the logical rule, the learning may well be analogical (on associative syntheses). Indeed, being M the bridge term, the situation of the figure triggers an analogical construction (second phase), if it is possible to recover (retrieval phase) a similar situation in which the bridge term is preserved.

Such a situation similar to the one in Figure 4 could be the relationship of the elements of the triad (B: Having gills, M: Mammal, C: Cetacean) that, in conjunction with the first triad (O, M, H), it would throw the analogy

H: O :: C: B

Underlying this analogical unit are the two following syllogisms

1.No M is an O

Every H is an M

Then, no H is an O.

2.No M is a B

Every C is an M

Then, no C is a B.

Making the analogy explicit, it can be shown the relevance of the “bridging” process. Indeed, that "no human is oviparous just as no cetacean has gills", forgetting where it derives from, that is, bridging, would lead us to think that such an analogy is somewhat "abstract". However, it has a legitimate reason because it derives from a situation already learned and justifiably related to the second member of the analogical proposition. But the relevance of the bridging that I want to show is that the genesis of this analogy comes from the relatively hyletic configuration. It is relatively hyletic because it is so at a level that supposes other more elementary levels that would account, for example, for "mammalian", "oviparity" and "hominity", which are implicitly underlying notions and which, in turn, they have their genesis in hyletic materials at their level. This genetic regression is the generation of meaning and learning.

It is possible, then, to design an effective procedure channeled into a current or "succession" of meanings that function hyletically (that is, like informed matter in its sense), in such a way that they are not diluted in the virtuality of the current itself but they are apperceptively “stored” (that is, along with their directionality as a “polarity”) to be retrievable and activatable (mappable) by the thematic situation to the present. The procedure I am referring to is learning by analogy in the field of processing linguistic terms.

Some guidelines for computational modeling of the analogy from a phenomenological approach

A dialogue about parallels between the neural network dynamics and the constitution of meaning by associative syntheses phenomenologically can be established, although the terms in which this can be done would depend on the perspective adopted, either from a "phenomenologization” of neural networks (or other machine learning models) or towards searching for formalization and modeling of phenomenological processes.

As far as the analogy is concerned, its modeling implies that of phenomenological processes since, from the perspective of this work, the analogy is based on passive and active syntheses, as well as on the Husserlian theory of whole and parts, including its formalization, such as that carried out by authors such as Fine, Simons and Casari. On the one hand, the analogy is not independent of such syntheses, while they do not require analogy, although some phenomenological processes can be described analogically. On the other hand, the phenomenological description uses elements that, within the unity of the analogy process, can be seen as parts and/or moments, as it can be shown above [6].

Application of the mediated foundation to obtain analog units of terms

The mediated Foundation is a substantial notion for the phenomenological foundation of the analogy. Three terms intervene in it, two of which are based on the third. Continuing with the usual notation, the procedure consists of considering, first, a triplet of terms (x⁺, x, y) and the proposition

xFy ∧ x ≤ x⁺ ∧ ¬ (x ≤ x⁺) → x⁺Fy

Second, analogously, consider another triplet of terms (w⁺, w, y) and the proposition

wFy ∧ w ≤ w⁺ ∧¬ (w ≤ w⁺) → w⁺Fy

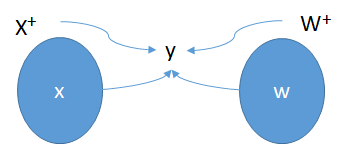
As it can be seen in Figure 5, the two triplets share a term, y. This term acts as a bridge between both triplets so that the mediated foundation can be applied in a parallel way.

Based on this schema and the following propositions

x ≤ x⁺ → x⁺WFx,y

w ≤ w⁺ → w⁺WFw

It can be gotten the analogical structure

x⁺WFx :: w⁺WFw

However, the mediated foundation applied in this way is not enough to guarantee analog unity. The bridging element “y” is what allows the analog equation to be consistent, and this is achieved to the extent that “y” expresses affinity between the pairs (X⁺, x), (W⁺, w).

An example of the application of this method is shown below.

Let the binomials be “weapon: Spear” and “pesticide: DDT”. A unifying element “y” can have a value between {hurt, harm, damage, …}. The functionality of the given pair, “Weapon: Spear” expressed by “y”, triggers the appearance of the analogous pair “pesticide: DDT”. There is an association in this process in which the bridging element "y" is the common term that allows configuring two analogous situations as shown below [7-10].

Let (X, τ) be a topological space,

Where X={w,s,p,d,h} and τ={{ },{h},{s,h},{d,h},{s,d,h}{w,s,p,d,h}}.

Let the sets A⊂ X, B ⊂ X, be A={w,s,h}, B={p,d,h}.

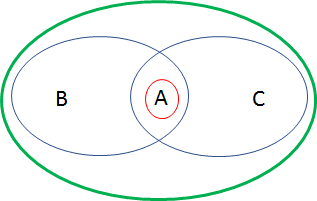
Then, an analogous situation like the one of (Figure 1) shows that there is a common term, h, to both sets A and B. 

On the other hand, sets A and B share the same closure which is the totality {w,s,p,d,h}

From this, it can be stated that what is needed by A and B to be independent is, according to the formal theory of whole and parts ∂(A)={p,d}; ∂(B)={w,s}

The interior subsets are Int(A)={s,h}; Int(B)={d,h}

The boundaries of the subsets are Fr(A)={w,p,d}; Fr(B)={w,s,p}

As it can be seen, the unifying element is “h”, which is the one that is missing in both boundaries and is common to both interior subsets Int(A) ∩ Int(B)={h}

The topological configuration of passive syntheses expresses the genesis of meaning. The interpretation of passive syntheses is an interpretation in terms of whole/parts. Thus, the analog unit actively obtained by the mediated foundation expresses what w:s is like, namely, p:d. But without the term "h" this likelihood is not understood. This term has its genesis by association. Now, the unifying element arises in the sphere of the association through the configuration of situations such as those illustrated in Figure 2. Obtaining this element can be achieved by Machine Learning processes [11].

To illustrate the above, consider the following passage from Lampert. "The unification of discrete contents is not achieved in the 'last moment' of a synthetic process, whether progressive or regressive, but the totality of temporality. (…) Only in the context of a double movement, forward towards the world as a whole and retrospectively towards pre-thetical horizons, does the syntheses establish its genesis”. While in the optimization processes of the objective function, within the connectionist paradigm of machine learning, the synthesis is reflected as convergence; within the symbolic paradigm, the synthesis is reflected as a certain topological situation in terms of sets and their elements [12].

The identification of what I have called the “bridge element” (h-term) is, in the light of neural network and deep learning models, that which is obtained through a process of convergence of vectorized terms that, in the case of processing of terms and pairs of terms is essential to the passive-active process I propose. In natural language processing, particularly in the handling of like terms, the process of word embedding in terms of other terms is a type of representation such that words with a similar meaning have a similar representation, as vectors whose dimensions correspond to certain characteristics or aspects of the terms (such as emotional connotation, gender, plurality, synonymy, antonymy, etc.) [13].

Pairs of terms processing

However, the search for similar terms is not the task that I propose and that is required, but that of common terms, bridging terms associated to a given pair of terms (as is the case of the term “h” (either harm, hurt, damage, etc. associated to the “Weapon: Spear” pair). A network can be “trained” to obtain “h” type terms through a type of term processing such as the one referred to. As I have pointed out, this convergent term is very relevant both in the passive phase itself and in the mediated foundation phase, and it is also the hinge element between both phases [14]. Within the typology of natural language processing problems, consider Yoav Goldberg's remarks in Neural Network Methods for Natural Language Processing, on which I can frame the tasks that would be implemented in a computational system. The mentioned typology establishes some tasks for the attention to specific problems regarding natural language (Goldberg, 65-67) that are akin to some of the interests and needs for modeling the analogy phenomenologically considered.

Words: From the processing of words (terms) there come up some problems of determination of ontological category, of the language they belong to, of use frequency, of similar terms, of orthography, etc. However, handling words in isolation, out of context, allows association between pairs of terms. From this binary association, bridge elements can be generated toward finding analogies.

Texts: In the processing of texts (phrases, sentences, paragraphs, or documents) the objectives that are usually proposed refer to their theme, their emotional charge, their authorship, their reliability, their intention, etc. This is a range of document classification problems. The interpretation task, which, as can be seen, has a substantial role in text processing, could be enhanced to the extent that the association process between pairs of terms is implemented and considered through an h-term.

Pairs of terms/words: By handling pairs of words one looks for questions of synonymy or translation. By handling pairs of texts, it is usually intended to determine the same authorship (or not), or else, the inference of one text from the other. Both similarity and contrast are fundamental elements in terms of passive genesis primary and secondary for which they are substantial elements, which are grounded phenomenologically, for the generation of analogies.

Relationship between two words: In (Goldberg) it is mentioned as purposes of this type of task, to find the grammatical positions of two terms concerning each other within a given text (subject, verb, direct object, etc.). Also, the task of verifying if a certain relationship exists between two terms. For example, “does the relation ‘purchase’ hold between words A and B in a given text?” (Goldberg 2017, 66).

•As it can be seen, searching for and obtaining “h” elements fits into this task by verifying that such an element is the convergent term for two pairs of words within a given text.

•On the other hand, the analogical relation between two terms is defined in terms of another pair of terms. So, this task, which is pointed out in (Goldberg 2017, 66), that of verifying that a given pair of terms support a certain relationship with each other, would mean for the model I propose that there is already a certain base of pairs of terms, already related according to such a relationship, generated by the parallel mediated foundation procedure. In this sense, the vectorization or encoding of each pair of terms would include, as a vector dimension, this relationship.

Conclusions

By what has been exposed in this work on the phenomenological foundation of analogy, looking to its modeling, I propose to recapitulate the following

•Analogy is a matter of gradation between identity and difference, a range in which resemblance or similarity fluctuates.

•Husserlian notions of passivity and the theory of wholes and parts are the conceptual platform to phenomenologically support the process of analogy.

•Establishing that A is to B as C is to D means that A is to B in the same way that C is to D. The pairs (A, B) and (C, D) support each other, they are reciprocally founded. The relation that exists in one pair is founded on that which exists in the other; both are founded and founding, although not at the same time. In the first instance, in the actual construction of the analogy, it is the already known pair that found.

•According to the previous point, it is necessary to consider that the treatment of an analogical relation can be given in the first moment, constructive, synthetic, of genesis; and another moment, of analysis (of the relationship already established).

•The analog process is conducted on a mediation scheme between its constituent elements. The relationship between the pair (a,b) of a member is given mediately to how the pair (c,d) is related. Phenomenologically, analog mediation occurs in terms of completeness of meaning. That is, the relationship that occurs in one member of the analogical expression makes sense in the same way as the pair of the best-known member. The grasp of the sense in the unknown relation of the pair (a,b) requires the grasp of the sense in the known relation (c,d). The phenomenological basis in this is the underlying notion of having-need-for, that is, the idea of the demand for a certain supplement. This notion is formally handled, in terms of the wholes and the parts, by the lock.

•The ideal of plenitude (closure) of the whole is constituted on systems of open wholes/parts. From the parts there is a demand—there is openness to—greater contextual coverage, while from the whole there is a demand—there is openness to—an internal articulation.

•The general process of modeling the analogy, within the treatment of linguistic terms of natural language that I propose, is a self-recursive process that allows the realization or updating of hyletic matter (what learning would be), developing between passivity and activity, as continuous phases, and from one to the other. In terms of the analogy, what is learned is the material retained and ready to form new learning; recoverable (retrieval) to be "processed", put in correspondence (mapping) with what is currently focused. The result of these two phases, the fused noematic material will be, after its schematization (abstraction) and its conformation as a noematic unit (re-representation), new hyletic matter, learned and ready for its recursion.

•This procedure transits between the passive and active phases, which I have outlined in the phases of representation of the synthesis of homo/heterogeneity, on the one hand, and construction of the analogy (analog unit), on the other. But the contents of synthesis—of the first-mentioned phase can be of different cognitive levels: From figures whose association is motivated merely by their shared regularity (similarity) to complex elaborations passing, for example, by syllogistic-type synthesis motivated by forms and logical figures.

•In short, then, a learning procedure by analogy is proposed in the field of processing linguistic terms, channeled into a current or "succession" of meanings that function hyletically (that is, as informable material in its sense), so that they are not diluted in the virtuality—of the current itself—but are “stored” apperceptively (that is, together with its directionality—as a kind of “polarity”) to be recoverable (retrievable) and activatable (mappable) by the situation theme to the present.

References

1. Goldberg Yoav (2017) Neural network methods for natural language processing. Morgan and claypool publishers pp: 1-309. [Crossref], [Google Scholar], [Indexed]
2. Husserl E (2001) Analyses concerning passive and active synthesis: Lectures on transcendental logic. Kluwer Academic Publishers 9: 14-66.
3. Lampert J (1995) Synthesis and backward reference in husserl's logical investigations. Springer Netherlands 131: 125-181. [Crossref], [Google Scholar].
4. Smith B (1982) Parts and moments studies in logic and formal ontology. München - Wien: Philosophia Verlag. [Crossref], [Google Scholar].
5. Gentner D, Forbus K (2011) Computational models of analogy. Cognitive Science 2: 266–276. [Crossref], [Google Scholar], [Indexed],
6. Husserl E (1984) Logische untersuchungen husserliana 19. Dordrecht: Springer Netherlands pp: LXVII, 958. [Crossref], [Google Scholar].
7. Husserl E (2001) Logical investigations. Trad. J. N. Findlay pp: 1-432. [Crossref], [Google Scholar], [Indexed]
8. Husserl E (2001) Analyses concerning passive and active synthesis: Lectures on transcendental logic. Kluwer Academic Publishers. [Crossref], [Google Scholar]
9. Husserl E (2013) Ideas relativas a una fenomenología pura y una filosofía fenomenológica. Libro primero. Traducción de Antonio Zirión 15: 269-279. [Crossref], [Google Scholar]
10. Smith B, Woodruff Smith Y (1995) The cambridge companion to husserl. Cambridge university press pp: 509-518. [Crossref], [Google Scholar]
11. Gentner D, Forbus K (2011) Computational models of analogy. Cogn Sci 2: 266–276. [Crossref], [Google Scholar], [Indexed] 
12. Larkey Levi B, Bradley CY (2003) CAB: Connectionist analogy builder.Cogn Sci 5: 781–94. [Crossref]  [Google scholar].
13. Smith B, Woodruff Smith Y (1995) The cambridge companion to husserl. Cambridge university press.   [Crossref], [Google Scholar].
14. Markman AB, Gentner D (2000) Structure mapping in the comparison process. Am J Psychol 113: 501-538.  [Crossref], [Google Scholar]