Keywords

Neutrosophic cubic soft set; Neutrosophic soft set; Cubic set; Internal neutrosophic Cubic soft set; External neutrosophic cubic soft set

Introduction

Neutrosophic set [1] grounded by Smarandache in 1998, is the generalization of fuzzy set [2] introduced by Zadeh in 1965 and intuitionistic fuzzy set [3] by Atanassov in 1983. In 1999, Molodstov [4] introduced the soft set theory to overcome the inadequate of existing theory related to uncertainties. Soft set theory is free from the parameterization inadequacy syndrome of fuzzy set theory [2], rough set theory [5], probability theory for dealing with uncertainty. The concept of soft set theory penetrates in many directions such as fuzzy soft set [6-9], intuitionistic fuzzy soft set [10-13], interval valued intuitionistic fuzzy soft set [14], neutrosophic soft set [15-18], interval neutrosophic set [19,20]. In 2012, Jun et al. [21] introduced cubic set combining fuzzy set and interval valued fuzzy set. Jun et al. [21] also defined internal cubic set, external cubic set, P-union, R-union, P-intersection and R-intersection of cubic sets, and investigated several related properties. Cubic set theory is applied to CI-algebras [22], B-algebras [23], BCK/BCI-algebras [24,25], KU-Algebras ([26,27], and semi-groups [28]. Using fuzzy set and interval-valued fuzzy set Abdullah et al. [29] proposed the notion of cubic soft set [29] and defined internal cubic soft set, external cubic soft set, P-union, R-union, P-intersection and R-intersection of cubic soft sets, and investigated several related properties. Ali et al. [30] studied generalized cubic soft sets and their applications to algebraic structures. Wang et al. [31] introduced the concept of interval neutrosophic set. In 2016, Ali et al. [32] presented the concept of neutrosophic cubic set by combining the concept of neutrosophic set and interval neutrosophic set. Ali et al. [32] mentioned that neutrosophic cubic set is basically the generalization of cubic set. Ali et al. [32] also defined some new type of internal neutrosophic cubic set (INCSs) and external neutrosophic cubic set (ENCSs) namely, 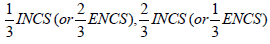. Ali et al. [32] also presented a numerical problem for pattern recognition. Jun et al. [33] also studied neutrosophic cubic set and proved some properties. In 2016, Chinnadurai et al. [34] introduced the neutrosophic cubic soft sets and proved some properties.

In this paper we discuss some new operations and new approach of internal and external neutrosophic cubic soft sets, and P-union, R-union, P-intersection, R-intersection. We also prove some theorems related to neutrosophic cubic soft sets.

Rest of the paper is presented as follows. Section 2 presents some basic definition of neutrosophic sets, interval-valued neutrosophic sets, soft sets, cubic set, neutrosophic cubic sets and their basic operation. Section 3 is devoted to presents some new theorems related to neutrosophic cubic soft sets. Section 4 presents conclusions and future scope of research.

Preliminaries

In this section, we recall some well-established definitions and properties which are related to the present study.

Definition 1: Neutrosophic set [1]

Let U be the space of points with generic element in U denoted by u. A neutrosophic set λ in U is defined as λ={<u, t^λ (u), i^λ (u), f^λ (u)>:u∈U} , where t^λ (u):U →]^- 0, 1⁺ [,i^λ (u):U →]^- 0, 1⁺ [, and f^λ (u):U →]^- 0, 1⁺ [ and − 0 ≤ t^λ (u)+ i^λ (u)+f^λ (u) ≤3⁺.

Definition 2: Interval value neutrosophic set [31]

Let U be the space of points with generic element in U denoted by u. An interval neutrosophic set A in U is characterized by truthmembership function t_A, the indeterminacy function i_A and falsity membership function f_A. For each u∈U, t_A (u), i_A (u), f_A (u) ⊆ [0, 1] and A is defined as

A={<u, [ t⁺A (u), t⁺A (u)], [ i⁻A (u), i⁺A (u)], [ f⁻A (u), f⁺A (u)]:u∈U}.

Definition 3: Neutrosophic cubic set [32]

Let U be the space of points with generic element in U denoted by u∈U. A neutrosophic cubic set in U defined as 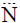={< u, A (u), λ (u) >: u∈U} in which A (u) is the interval valued neutrosophic set and λ(u) is the neutrosophic set in U. A neutrosophic cubic set in U denoted by 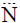= <A, λ>. We use C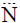(U) as a notation which implies that collection of all neutrosophic cubic sets in U.

Definition 4: Soft set [4]

Let U be the initial universe set and E be the set of parameters. Then soft set FK over U is defined by F_K ={< u, F (e)>: e ∈ K, F (e) ∈P (U)}

Where F: K → P (U), P (U) is the power set of U and K ⊂ E.

Definition 5: Neutrosophic cubic soft set [34]

A soft set 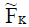is said to be neutrosophic cubic soft set iff 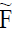is the mapping from K to the set of all neutrosophic cubic sets in U (i.e., C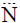(U) ).

i.e. 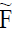: K→C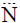(U) , where K is any subset of parameter set E and U is the initial universe set.

Neutrosophic cubic soft set is defined by

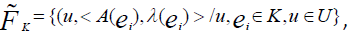
Where, A(e_i) is the interval valued neutrosophic soft set and λ(e_i) is the neutrosophic soft set.

Definition: Internal neutrosophic cubic soft set (INCSS)

A neutrosophic cubic soft set 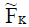is said to be INCSS if for all e_i∈ K E

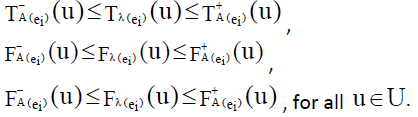
Definition: External neutrosophic cubic soft set (ENCSS)

A neutrosophic cubic soft set 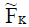is said to be ENCSS if for all e_i∈ K E

,

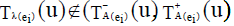Some theorem related to these topics

Theorem 1

Let 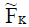be a neutrosophic cubic soft set in U which is not an ENCSS. Then there exists at least one e_i ∈ K ⊆ E for which there exists some u∈U such that

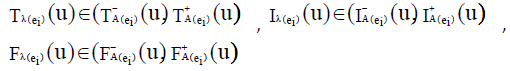
Proof

From the definition of ENCSSs, we have

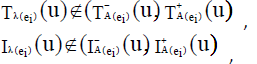
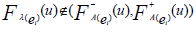, for all u∈U, corresponding to each e_i∈ K ⊆ E.

But given that 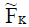is not an ENCSS, so at least one ei ∈ K ⊆ E.

There exists some u∈U such that 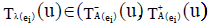, 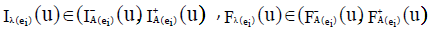. Hence the proof is complete.

Theorem 2

Let 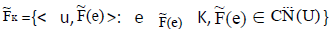be a NCSS in U. If 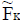is both an INCSS and ENCSS in U for all u∈U, corresponding to each e_i ∈ K, then, 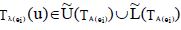, ,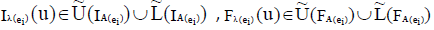where

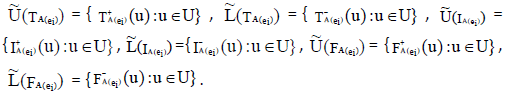
Proof

Suppose 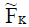be both an INCSS and ENCSS corresponding to each e_i ∈ K and for all u∈U. We have , , ,

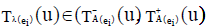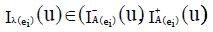Again by definition of ENCSS corresponding to each e_i K ∈ and for all u∈U, we have

, ,

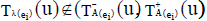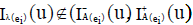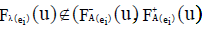
Since 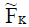is both an ENCSS and INCSS, so only possibility is that, ,

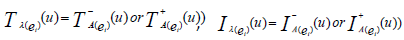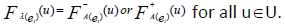
Hence proved.

Definition

Let 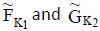be two neutrosophic cubic soft sets in U and K₁, K₂ be any two subsets of K. Then, we define the following:

1.

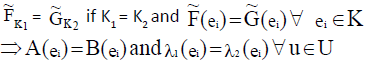
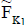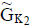2. If and are two NCSSs then we define P- order as 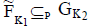iff the following conditions are satisfied:

i. K₁ ⊆ K₂, and

ii.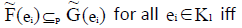

A(e_i) B(e_i) and 1 (e ) 2 (e ) u U ⊆ λ ⊆λ ∀ ∈ corresponding to each

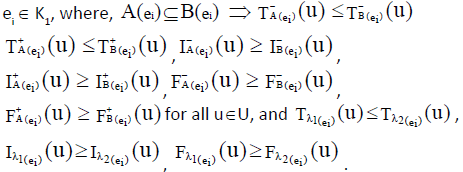
3. If are two neutrosophic cubic soft sets, then we
define the R-order as 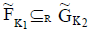iff the following conditions are satisfied:

i. K₁ ⊆ K₂ and

ii. 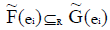for all ei ∈ K1 iff 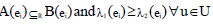corresponding to each e_i ∈ K₁.

Definition

Let 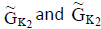be two NCSSs in U and K1, K2 be any two subsets of parameter set K. Then we define P-union as 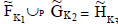, where K₃ ∈ K₁∪ K₂,

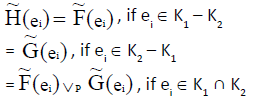
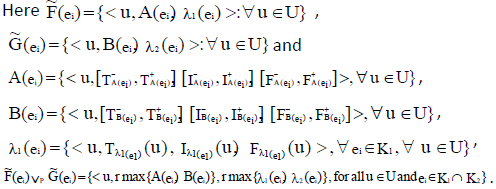
Definition

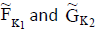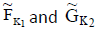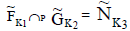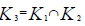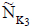Let be two NCSSs in U and K₁, K₂ be any two subsets of parameter set K. The P-intersection of is denoted by where and defined as=

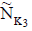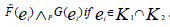
Here,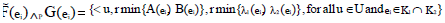

Definition: Compliment

The compliment of 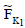denoted by 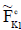is defined by

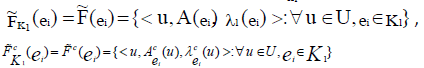
Where,

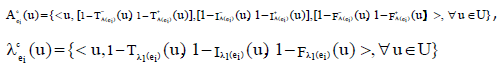
Some properties of P-union and P-intersection

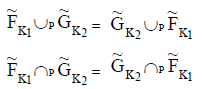
Proof 1:

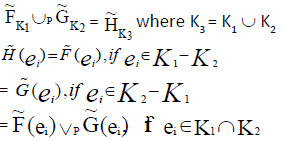
Here,

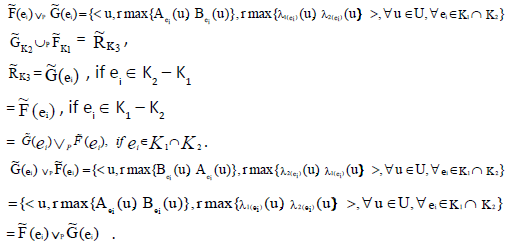
Hence the proof.

Proof 2:

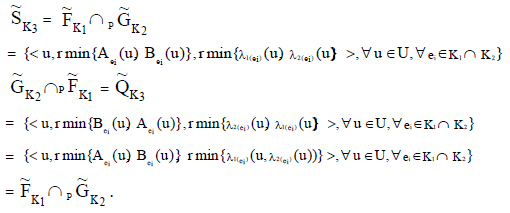
Hence the proof.

Definition: R-union and R-intersection

Let 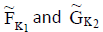be two NCSSs over U. Then R-union is denoted as 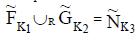, where K₃ = K₁∪ K₂ and 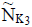. Then R-union is defined as

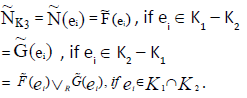
Here 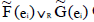defined as

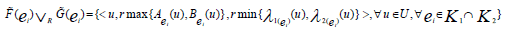
R-intersection is denoted as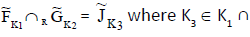

K₂.Then R-intersection is defined as:

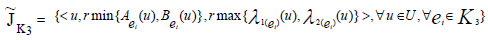
Theorem 3

Let U be the initial universe and I, J, L, S any four subsets of E, then for four corresponding neutrosophic cubic soft sets 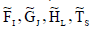the following properties hold

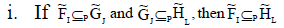
Proof: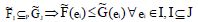

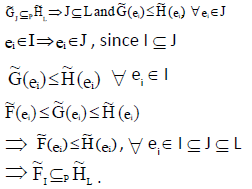
Hence the proof.

ii.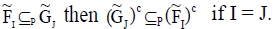

Proof: If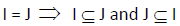

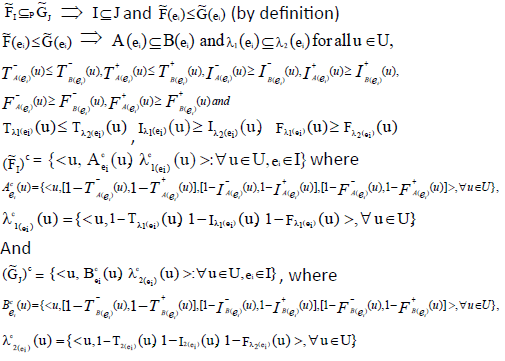
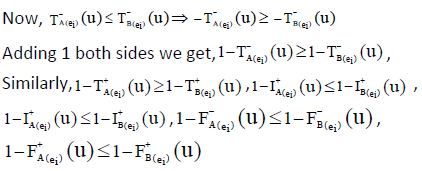(1)

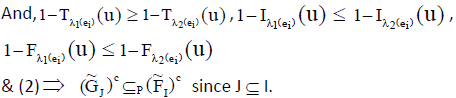(2)

Hence the proof.

Theorem 4

Let 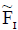be a NCSS over U,

If 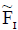is an INCSS then 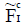is also an INCSS.

If 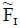is an ENCSS then 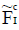is also an ENCSS.

Proof

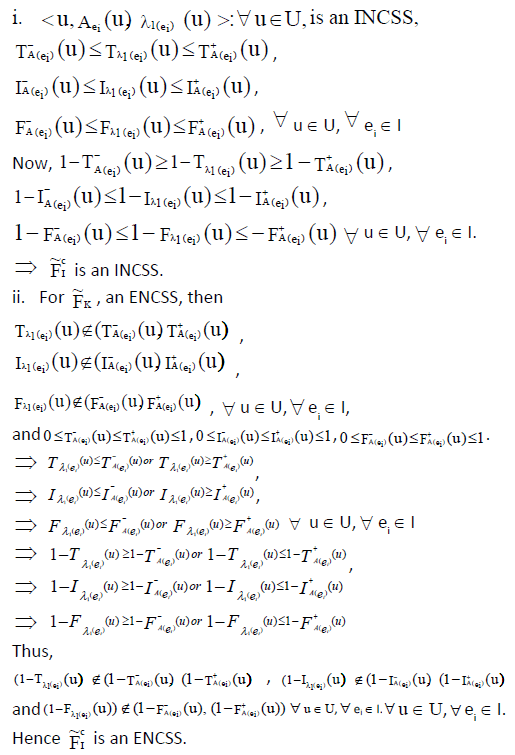
Theorem 5

Let and be any two INCSSs then

is an INCSS.

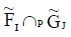is an INCSS.

Proof

Since 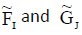are INCSSs, so for 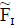we have

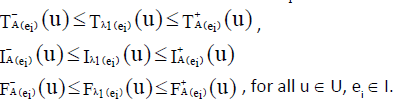
Also for 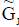we have

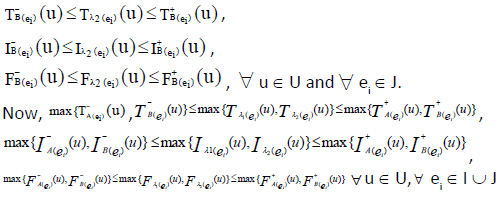
Now by the definition of P-union 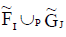is an INCSS.

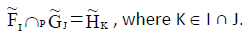
ii. Now, 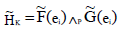and by definition,

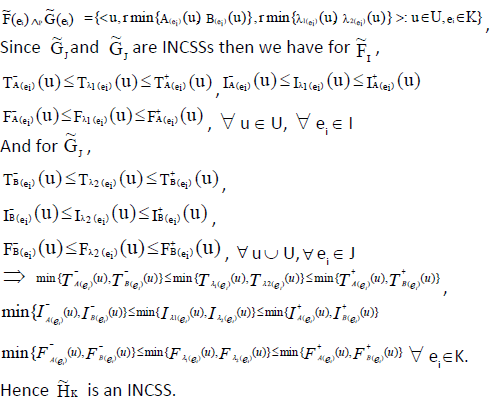
Theorem 6

Let 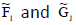be any two INCSSs over U having the conditions:

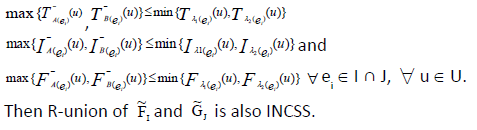
Proof

Since 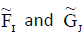are INCSSs in U.

So for 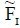, we have

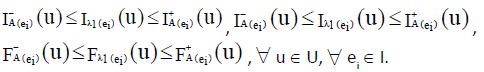
Also for 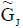we have

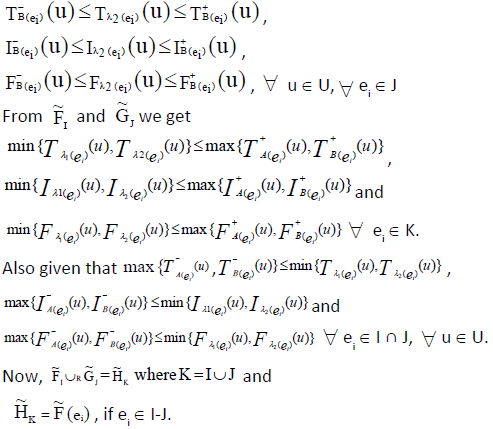
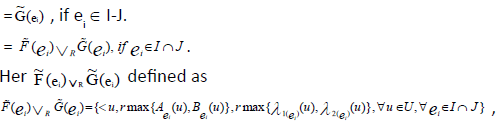
Since 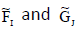are INCSSs so from the given condition and definition of INCSS we can write,

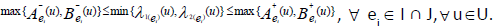
If e_i ∈ I - J or ei ∈ J - I then, the result is trivial.

Thus 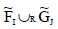is an INCSS.

Theorem 7

Let 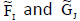be any two INCSSs over U satisfying the condition: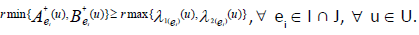

Then 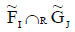is an INCSS.

Proof

Since 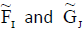are INCSSs in U,

we have, 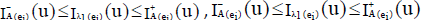and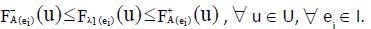

Also for 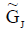we have, 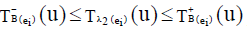, 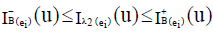and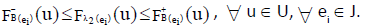

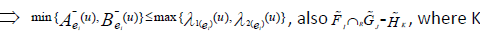
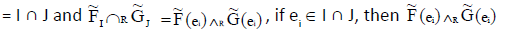
defined as

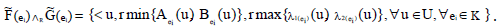
Given condition that 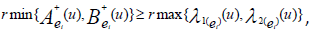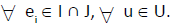Thus from given condition and definition of INCSSs

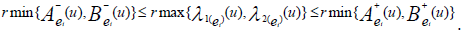
Hence 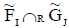is an INCSS.

Theorem 8

Let 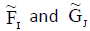be any two ENCSSs then

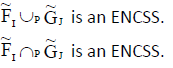
Proof

Since 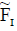and are ENCSSs, we have

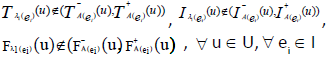
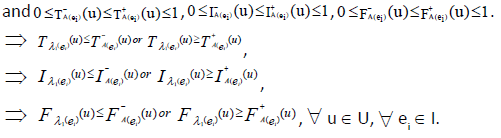
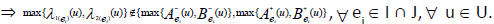
Now by definition of P-union, .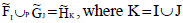

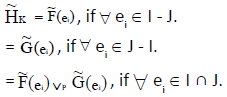
Here 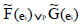defined as

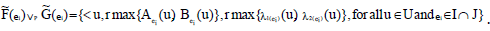
Thus

For e_i ∈ I - J or e_i ∈ J - I these results are trivial.

Hence the proof.

ii. Since 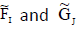are ENCSSs, then

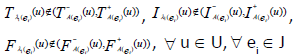
and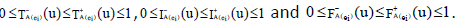

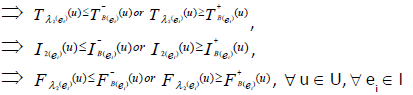
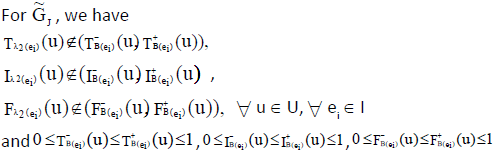
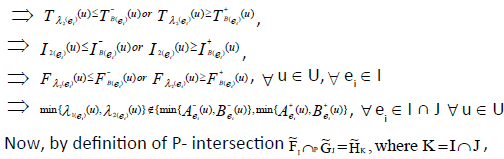
we have

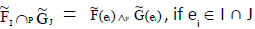
Here 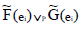defined as

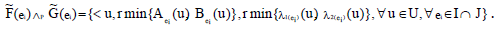
Thus 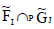is an ENCSS.

Theorem 9

Let 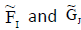be any two INCSSs in U such that

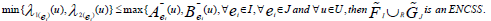
Proof:

Since 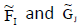are INCSSs in U.

we have,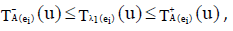

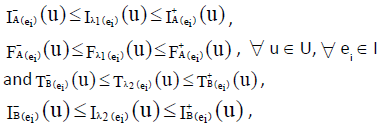
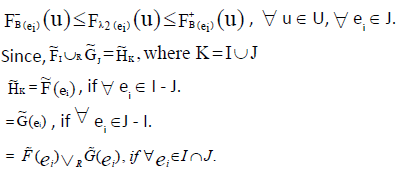
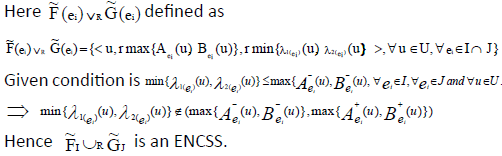
Definition

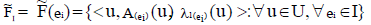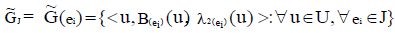Let and are two NCSSs in U. We defined new NCSSs by interchanging the neutrosophic part of the two NCSSs. We denoted its by 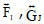and defined by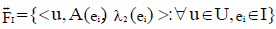, 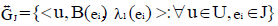respectively.

Theorem 10

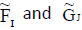are ENCSSs and 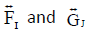are INCSSs in U. Then 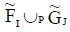is an INCSS in U.

Proof

Since 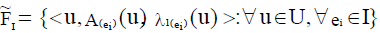and 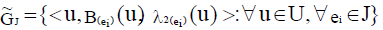are ENCSSs,

we have

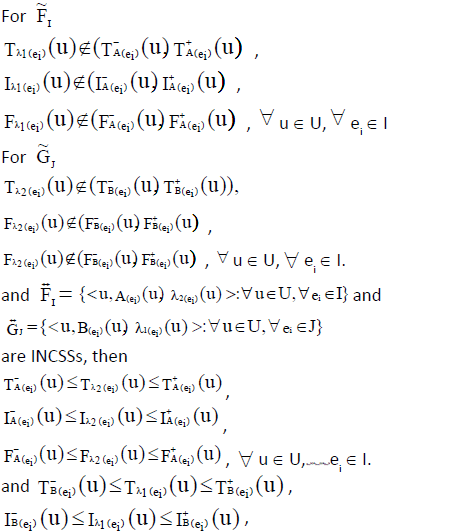
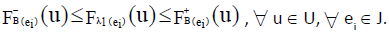By the definition of ENCSSs and INCSSs all the possibility are as under:

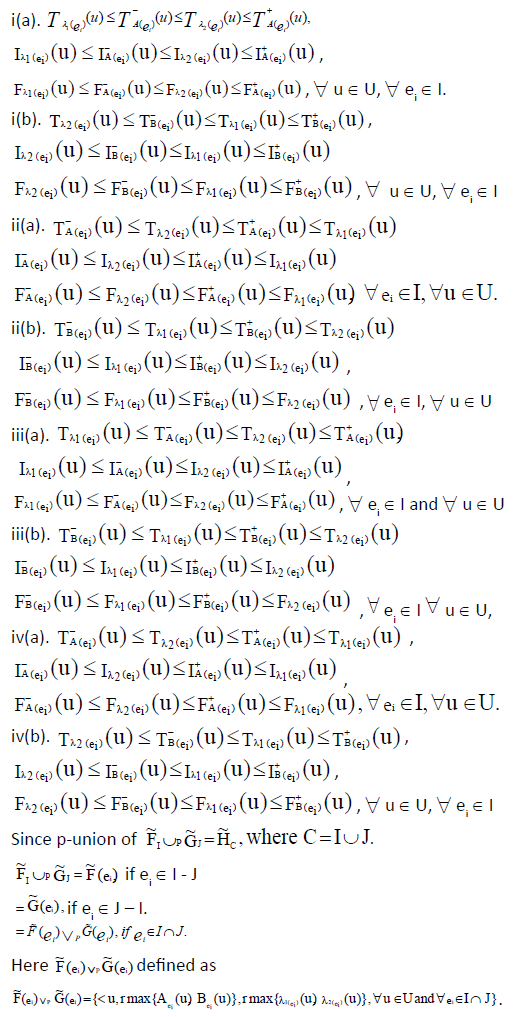
Case 1

If 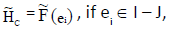then from i(a)., and ii(a). We have

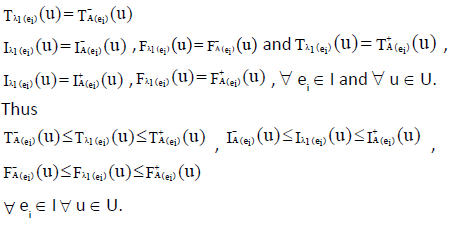
Case 2

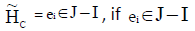then from i(b) and ii(b). , we have

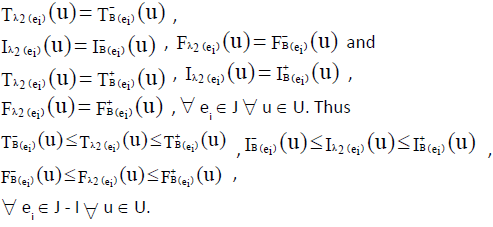
Case 3

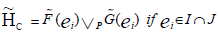, then from i(a) and i(b)., we have

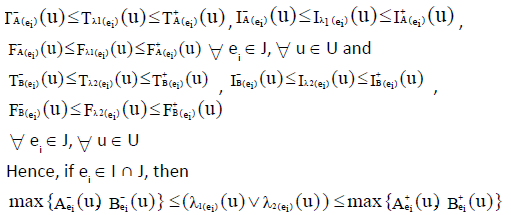
in all the three cases.

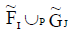is an INCSS in U.

Conclusion

In this paper we have defined some operations such as P-union, P-intersection, R-union, R-intersection for neutrosophic cubic soft sets. We have also defined some operation of INCSSs and ENCSSs. We have proved some theorems on INCSSs and ENCSSs. We have discussed various approaches INCSSs and ENCSSs. We hope that proposed theorems and operations will be helpful to multi attribute group decision making problems in neutrosophic cubic soft set environment.

References

1. Smaramdache F (1998) A unifying field in logics. neutrosophy: Neutrosophic probability set and logic. Rehoboth: American research press.
2. Zadeh LA (1965) Fuzzy sets. Information and Control 8: 338-353.
3. Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets and Systems 20: 87-96.
4. Molodtsov DA (1999) Soft set theory-first results. Computers and Mathematics with Applications37: 19-31.
5. Pawlak Z (1982) Rough sets.  International journal of information and computer sciences 11: 341-356.
6. Agman NC, Deli I (2012) Means of FP-soft sets and its applications. Hacettepe Journal of Mathematics and Statistics 41: 615-625.
7. Agman NC, Deli I (2012) Product of FP-soft sets and its applications. Hacettepe Journal of Mathematics and Statistics 41: 365-374.
8. Feng Q, Zheng W (2014) New similarity measures of fuzzy soft sets based on distance measures. Annals of Fuzzy Mathematics and Informatics 7: 669-686.
9. Maji PK, Biswas R, Roy AR (2001) Fuzzy soft sets. Journal of Fuzzy Mathematics 9:589-602.
10. Bora M, Bora B, Neog TJ, Sut DK(2014) Intuitionistic fuzzy soft matrix theory and it' s application in medical diagnosis.  Annals of Fuzzy Mathematics and Informatics 7: 143-153.
11. Jiang Y, Tang Y, Chen Q(2011) An adjustable approach to intuitionistic fuzzy soft sets based decision making. Applied Mathematical Modelling 35: 824-836.
12. Maji PK, Biswas R, Roy AR (2004) On Intuitionistic fuzzy soft sets. The journal of Fuzzy Mathematics 12: 669-683.
13. Yang YW, Qian T (2013) Decision-making approach with entropy weight based on intuitionistic fuzzy soft set. Annals of Fuzzy Mathematics and Informatics 6: 415-424.
14. Mukherjee A, Saha A (2013) Interval-valued intuitionistic fuzzy soft rough sets. Annals of Fuzzy Mathematics and Informatics 5: 533-547.
15. Broumi S, Deli I, Smarandache F (2014) Neutrosophic Parameterized Soft Set Theory and Its Decision Making. International Frontier Science Letters 1: 1-11.
16. Deli I, Toktas Y, Broumi S (2014) Neutrosophic Parameterized Soft Relations and Their Applications. Neutrosophic Sets and Systems 4: 25-34.
17. Maji PK (2013) Neutrosophic soft set. Annals of fuzzy mathematics and informatics 5: 157-168.
18. Maji PK (2012) A neutrosophic soft set approach to a decision making problem. Annals of Fuzzy Mathematics and Informatics 3: 313-319.
19. Broumi S, Deli I, Smarandache (2014) Relations on interval valued neutrosophic soft sets. Journal of New Results in Science 5: 01-20.
20. Broumi S, Deli I, Smarandache (2014) Distance and similarity measures of interval neutrosophic soft sets. Critical Review 8: 14-31.
21. Jun YB, Kim CS, Yang KO (2012) Cubic sets. Annal of Fuzzy Mathematics and Informatics 4: 83-98.
22. Ahn SS, Kim YH, Ko JM (2014) Cubic subalgebras and filters of CI-algebras. Honam Mathematical Journal 36: 43-54.
23. Senapati T, Kim CS, Bhowmik M, Pal M (2015) Cubic subalgebras and cubic closed ideals of B-algebras. Fuzzy Information and Engineering 7: 129-149.
24. Jun YB, Lee KJ (2010) Closed cubic ideals and cubic subalgebras in BCK/BCI-algebras. Applied Mathematical Sciences 4: 65-68.
25. Jun YB, Lee KJ, Kang MS (2011) Cubic structures applied to ideals of BCI-algebras. Computers & Mathematics with Applications62: 3334-3342.
26. Akram M, Yaqoob N, Gulistan M (2013) Cubic KU-subalgebras. International Journal of Pure and Applied Mathematics 89: 659-665.
27. Yaqoob N, Mostafa SM, Ansari MA (2013) On cubic KU-ideals of KU-algebras. ISRN Algebra Art.
28. Jun YB, Khan A (2013) Cubic ideals in semigroups. Honam Mathematical Journal 35: 607-623.
29. Abdullah S, Khan I, Aslam M (2012) A new approach to soft set through applications of cubic set.
30. Ali A, Jun YB, Khan M, Shi FG, Anis S (2015) Generalized cubic soft sets and their applications to algebraic structures. Italian Journal of Pure and Applied Mathematics 35: 393-414.
31. Wang H, Smarandache F, Zhang YQ, Sunderraman R (2005) Interval Neutrosophic Sets and logic: Theory and Applications in Computing. Hexis, Neutrosophic book series.
32. Ali M, Deli I, Smarandache F (2016) The theory of neutrosophic cubic sets and their applications in pattern recognition. Journal of Intelligent and Fuzzy Systems 30: 1957-1963.
33. Jun YB, Smarandache F, Kim CS (2017) Neutrosophic cubic sets.New Mathematics and Natural Computation 13: 41-54.
34. Chinnadurai V, Swaminathan A, Anu B (2016) Some properties of Neutrosophic cubic soft set. International Journal of Computational Research and Development 1: 113-119.