Keywords

Physical Informatics; Entropic Uncertainty Relations (EUR); Information Entropy; Shannon Entropy; Von Neumann Entropy; Information Energy; Quantum Information Entropy; Maxwell’s Demon

Introduction

Physics, as a discipline is concerned with the systematic study of the physically measurable properties of the system and the interactions among themselves leading to a change in the aforementioned physically measurable properties. We proceed by defining abstract variables or parameters, depending on our observations, to specify uniquely the configuration of the system by quantifying those variables or parameters in terms of the physical measurements carried out on the system under consideration.

One such variable/parameter (which we shall hereby call a quantity) that we have found very useful, due to certain properties it possesses; to specify the configuration of the system and to study its dynamics and interactions with other systems is Energy. The field of Physics that deals with the study of the dynamics of and the interactions among the systems in terms of energy is known as Thermodynamics or Energetics.

In the branch of Physical Informatics, we study the behavior and properties of systems in terms of a physical quantity (variable) called Information. This presents us with the abstract formalism that can be used for the analysis of a wide variety of systems.

Origin

In 1867, Sir James Clark Maxwell came up with a thought experiment in the field of statistical physical called the “Maxwell’s Demon”, the consequences of this thought experiment apparently violated the Second Law of Thermodynamics, thereby creating a paradox ,since the aforementioned law is one of the most fundamental laws of Physics. The field of Physical Informatics originated in response to this paradox.

Hereby, we discuss in detail the thought experiment of the “Maxwell’s Demon”, the paradox and its eventual resolution.

The thought experiment

Let us consider an insulated container of volume V containing a gas at temperature T. Now an insulating partition is introduced in the container that divides the entire volume of the container in two equal halves (of volume V/2). The partition contains a microscopic trapdoor that can open reversibly (no network is done in the process of opening and then closing the trapdoor). A very small (microscopic), intelligent entity or device known as the “demon” is placed beside the trapdoor controls its opening and closing.

Now let the initial Root Mean Square (RMS) velocity of the gas molecules be vi, the RMS velocity of the gas molecules in side 1 and 2 of the container be v1 and v2 respectively. Since initially the gas molecules were uniformly distributed throughout the volume of the container, therefore v1=v2=vi.

Now when a molecule having velocity greater than vi approaches the trapdoor from side 2, the demon opens the door and lets it pass to side 1, and when a molecule having velocity lesser than vi, approaches the trapdoor from side 1, the demon opens the trapdoor and lets the molecule pass to side 2. At all other instances the trapdoor remains closed.

Since the trapdoor operates reversibly, therefore no network is done by the demon in opening and then closing it.

Now the aforementioned process tends to increase v₁ above v_i and decrease v₂ below v_i; and the longer the above process is carried out, the higher v₁ rises and lower v₂ falls [1-7].

Therefore the average Kinetic Energy of the molecule in side 1 increases and that of molecules in side 2 decreases, thereby resulting in a rise in temperature of side 1 and a fall in temperature of side 2, without any net work being done in the process.

Thus, effectively we end up transferring heat energy from the side at lower temperature to the side at higher temperature without doing any network on the system, which is in clear violation of the Second Law of Thermodynamics [Clausius’s Statement] [2].

According to the Clausius’s Statement of The Second Law of Thermodynamics, “It is impossible to construct a refrigerator that, operating in a cycle, will produce no effect other than the transfer of heat from a lower temperature reservoir to a higher temperature reservoir”.

Thus, in carrying out the aforementioned process, the net entropy of the closed system (the insulated container) decreases with time. This results in the paradox that we mentioned before because the net entropy of a closed system should always increase.

Resolution of the paradox

The paradox put forth by the thought experiment of the “Maxwell’s Demon” is resolved by taking into consideration the phenomenon of information processing that is carried out in the memory of the “demon” in order to perform the task assigned to it [8].

The aforementioned Information Processing consists of logical operations carried out on the input received by the device/ machine and the storage of the processed output in its memory followed by the final erasure of the information at the end of the complete task, all realized and implemented through physical systems. But for this to happen, there has to be a one-to-one correspondence between the logical states (representing the information being obtained, processed, and stored) and the physical states (physical configuration) of the system being used for the aforementioned information processing.

Now let us consider one particular physical state of the system as the standard state or the default state of the system representing null information content, as information processing is carried out, the system acquires particular physical configurations, each uniquely representing a logical state of the system.

Each logical operation carried out is represented by an injective mapping from one logical state to another and is realized by a reversible physical process that takes the system from one physical configuration to the other; however the previous state remains traceable by the inverse (reverse) mapping realized by the reverse physical process carried out on the output state.

However, the erasure (deletion) of information from the memory carried out by resetting the final state of the system to the standard state through an irreversible physical process. Since it is not possible to regain the preceding state from the default/ standard state due to the lack of a unique inverse mapping, therefore we can conclude that this process leads to a loss of information.

As discussed above, loss of information carried out by the logically irreversible process of deletion is implemented by a physically irreversible process; now since a physically irreversibly process is always associated with an increase in entropy of the closed system, therefore loss of information results in an increase in entropy of the system; consecutively a gain in information is associated with a decrease in entropy (total entropy of the system however still increases) of the system due to information.

The amount of Information contained in a system is equal to the amount of physical entropy generated due to the physically irreversible process associated with the logically irreversible process of deletion or erasure of the information from the memory of the system. Therefore we can regard Information as negative of entropy or “Negentropy”.

Information loss due to interaction

A particular logical state of a system is uniquely represented by a physical micro configuration (microstate) of the system, that is, if the system remains in a single microstate, then the memory of the system contains the single associated logical state and this represents the maximum amount of information that can be stored in the system [3].

However, when we allow the internal components of the closed system to interact with each other by reducing the internal constraints of the system, thereby increasing the internal degrees of freedom of the system, the system no longer remains in a single microstate. Its micro configuration keeps changing with time within a certain range (due to limited increase in internal degrees of freedom).

Hence such states store lesser amount of information. Therefore we can conclude that interactions lead to a decrease in the amount of information that can be stored in a system.

Measures of Information Content

Entropy

In the previous section, we have already shown how entropy acts as a measure of the information content of a system. In this section we will discuss three of the most commonly used forms of Information Entropy.

Shannon entropy: For Classical Systems, the amount of information contained is given in terms of the number of microstates present in the macrostate or the probability of occurrence of macrostates of the system containing an ensemble of classical sub-systems. It is defined as follows:

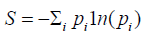
p_i: probability of occurrence of the ith macrostate.

Von neumann entropy: When we have a classical ensemble of quantum states, the amount of information contained or stored in the system is given by Von Neumann Entropy [4], which is defined in terms of the density operator as:

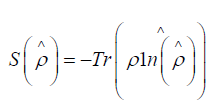
Quantum information entropy: Information can also be stored in a pure quantum state in terms of the probability amplitudes associated with each of the Eigen kets of the operator which is used as the basis for the expansion of the pure quantum state [5].

It is given by:

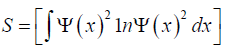
But the complete information about the systems behavior in the phase space is given by the simultaneous specification of the values of the associated pair of the conjugate variables to the extent permitted by Heisenberg’s Uncertainty Relations. Therefore the total amount information stored in the system is the sum total of the amount of information stored in terms of each of the two associated conjugate variables.

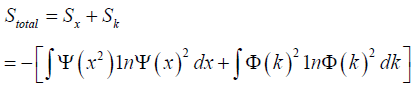
Information energy

Onicescu Introduced another measure of the amount of Information contained in a system known as Information energy, and it is defined as follows:

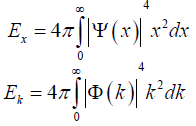
We can define another form of information entropy in terms of information energy:

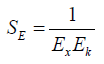
Application

Calculating the total entropy of N identical non- interacting particles in n dimensions that are symmetrical with respect to each other.

We consider a Gaussian wave function in the position basis; and since the particles are non- interacting, therefore the wave function in the momentum basis is also a Gaussian function of identical nature [6].

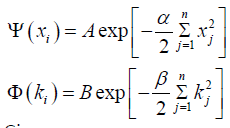
Given

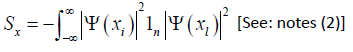
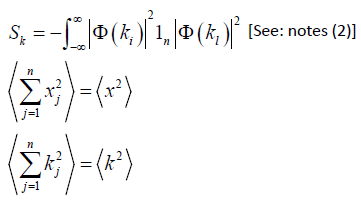
Derivation:

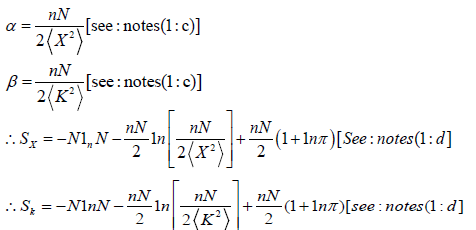
Now:

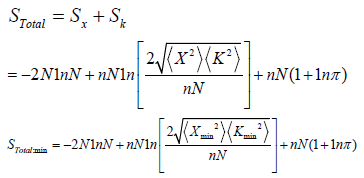
But from Heisenberg’s Uncertainty Relation, we have:

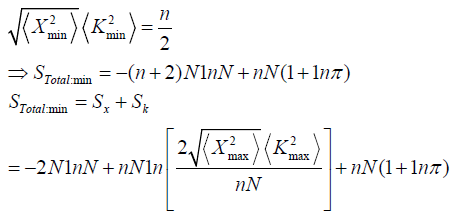
Therefore we have:

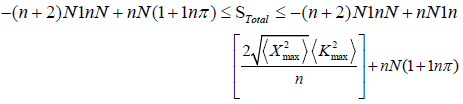
This is the Entropic Uncertainty Relation (EUR) for N particles in n dimensions

Notes 1:

Given:

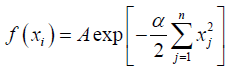
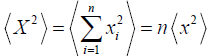
The constraint equation:

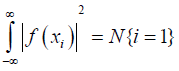
The definition of Information Entropy:

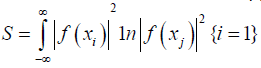
Determining the relation between A and α : imposing the number of particle constraint [ given(c)]

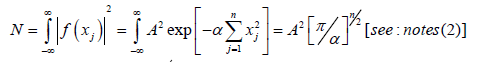
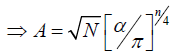
Determining α in terms of n, N and 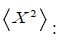imposing the given condition

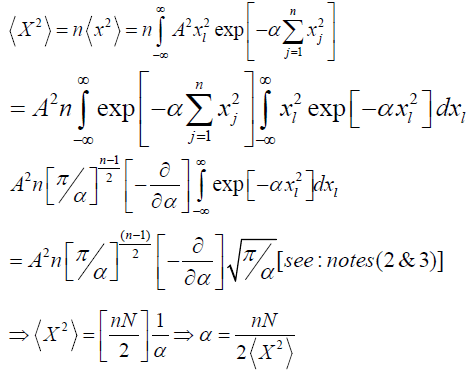
Determining S in terms of n, N and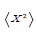

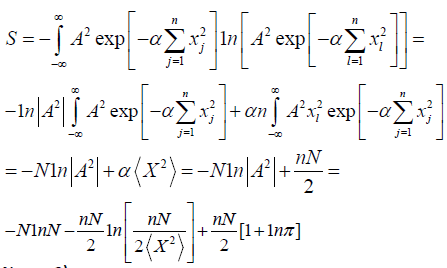
Notes: 2)

We have defined:

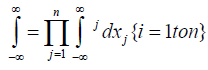
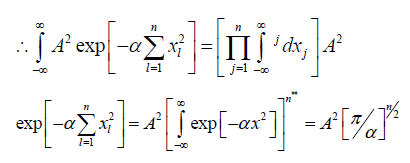
[See notes (3)]

**Since the x_i’s are independent of each other, therefore the functional form involves the product of the exponentials of ^x_i (s) and they are symmetric in nature.

Notes: 3)

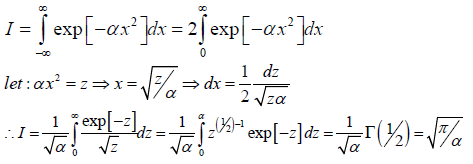
Results

In the previous section we have derived the Entropic Uncertainty Relation for N identical noninteracting bodies in n dimensions:

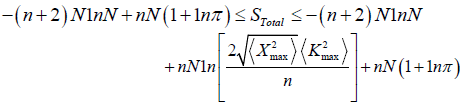
Now we verify our result by comparing it with the established result for n = 3:

According to our derivation, we get;

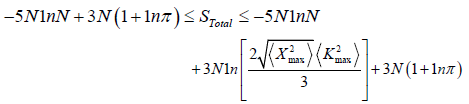
This result is in complete agreement with the established result; hence our result is verified for 3- dimensions.

Using the formula we have derived in this paper for EUR, we establish the EUR(s) in the lower dimensions, that is, 1 and 2 dimensions.

For 2 dimensions:

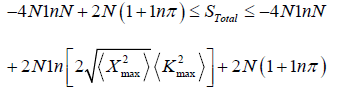
For 1 dimension:

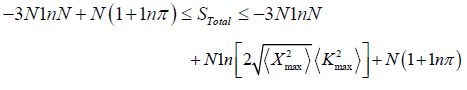
Conclusion

The EUR derived here are more fundamental than Heisenberg’s Uncertainty Relations because EUR(s) are independent of the state of the system, however it is not always so for Heisenberg’s Uncertainty Relations.

References

1. Blundell SJ Blundell KM (2006) Concepts in Thermal Physics.
2. Zeemansky MW, Dittman RH (2017) Heat and Thermodynamics (8^th edn).
3. Panos CP, Massen SE, Moustakidis CHC (2002) Universal trend of the Information entropy of a fermion in a mean field.
4. Massen SE, Panos CP, Moustakidis CHC (2002) Universal property of the Information entropy in fermionic and bosonic systems.
5. Massen SE Panos CP (2001) A link of entropy and kinetic energy for quantum many body systems. Phys Lett A 280: 65-69.
6. Panos CP, Massen SE (1998) Universal property of the Information entropy in atoms, nuclei and atomic clusters. Phys Lett A 246: 530-533.
7. Panos CP, Massen SE (2006) Information-Theoretic Methods in Correlated Bosons in a trap.
8. Maruyama K, Vedral V (2009) The physics of Maxwell’s demon and information. Rev Mod Phys 81.