ISSN : 0976-8505
Der Chemica Sinica
Energy and Laplacian Energy-Like Invariant of Unicyclic Molecular Graphs
Masood Ur Rehman*, Muhammad Riaz
University of Science and Technology of China, School of Mathematical Sciences, Hefei, An-hui, 230026, P.R. China
Abstract
Let Un be the set of unicyclic molecular graphs with 3 ≤ n ≤ 8 vertices. We show that the cycle Cn has maximal Laplacian-energy-like invariant (LEL) in Un. The authors partially proving that the conjecture hold for any unicyclic molecular graph in Un, where 3 ≤ n ≤ 8 Moreover, we show that Cn has maximal energy (E) in Un for 3 ≤ n≤7, but for n=8 this is not true.
Keywords:
Molecular graphs, Laplacian energy-like invariant, Energy
Introduction
The total π-electron energy E, as calculated within the Huckel molecular orbital (HMO) model, is one of the most thoroughly studied quantum-chemical characteristics of large polycyclic conjugated molecules. Details on the theory and applications of E can be found in the literature [1-3] and in the references cited therein. It was recognized a long time ago that the various π-electron descriptors of HMO model, including E, can be calculated from the eigenvalues λ1, λ2,..., λn of the underline molecular graph [4,5]. In particular, in the case of alternant hydrocarbons.
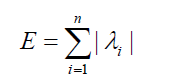 (1)
(1)
Where, as usual [1,2,4,5] E is expressed in the units of the HMO carbon-carbon resonance integral β. Formula (1) served as a motivation for the definition of the so-called graph energy. Namely, whereas within the HMO model E is meaningful only in the case of a restricted class of molecular graphs [5], the right-hand side of (1.1) is a well-defined quantity for all graphs. In view of this, the energy of a graph (also denoted by E) is defined as the sum of the absolute values of all eigenvalues of this graph, and this definition extends to all graphs. This seemingly insignificant change in the interpretation of Equation. (1) resulted in a great expansion of research in this area and has advanced the theory of total π-electron energy greatly; for details see the reviews [1,6] and some of the most recent publications dealing with graph energy [7-13].
By equation (1), the graph energy is defined in terms of the graph eigenvalues λ1, λ2
,..., λn. Recall that these are just the eigenvalues of the adjacency matrix [14]. Motivated by the success of the graph energy concept, and in order to extend it to the Laplacian eigenvalues, the Laplacian energy LE(G) was put forward, defined as
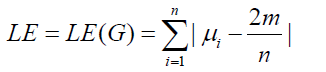 (2)
(2)
Where G is a graph with n vertices and m edges, and μ1, μ2,….., μn are its Laplacian eigenvalues [15]. The Laplacian energy has two major drawbacks: Namely, neither LE (G1 ∪ G2)=LE (G1) + LE (G2) holds in the general case, for G1 ∪ G2 being the graph consisting of two disconnected components G1 and G2, nor is the condition LE (G ∪ K1)=LE (G), where K1 is the graph with single vertex, satisfied. In order to overcome these difficulties, Liu and Liu invented the Laplacian energy-like invariant LEL (G), defined as [16].
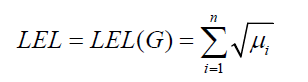 (3)
(3)
Indeed, the relations LEL (G1 [ G2)=LEL(G1) + LEL (G2) and LE(G ] K1)=LE(G) are generally vaild.
The theory of LEL is nowadays well developed; details and further references can be found in the review [17]. In particular, numerous correlations between LEL and physico-chemical properties of alkanes were reported [18]. It was shown that, in spite of its name, LEL resembles more the total π-electron energy than the Laplacian energy LE [19]. It is known that the main parameters determining the value of the total π-electron energy are n (= the number of carbon atoms, i.e, the number of vertices of the molecular graph) and m (= the number of carbon- carbon bonds, i.e, the number of edges of the molecular graph) [1,20].
In [21], Stevanovi´c studied the LEL of trees (trees are connected acyclic graphs). In that paper he conjectured the following conjecture as well
Conjecture 1.1 Among unicyclic molecular graphs on n vertices, the cycle Cn has maximal Laplacian energy-like invariant.
The main purpose of the present paper is to give the partial proof of the conjecture (1.1). That is we will prove that the conjecture 1.1 is true for 3 ≤ n ≤ 8. Moreover, we will show that among molecular unicyclic graphs the cycle Cn has maximal energy E for 3 ≤ n ≤ 7 but for n=8 it is not true. Where n is the number of vertices in the unicyclic molecular graph.
For unexplained terminology see the following subsection
Definitions: Let G=(V, E) be a simple connected molecular graph with vertex set V={v1, v2,..., vn} and edge set E={e1, e2,..., en}. Its adjacency matrix A(G)=(aij) is defined as n × n matrix (aij), where aij=1 if vi is adjacent to vj; and aij=0, otherwise. Denote by d(vi) or dG(vi) the degree of the vertex vi (number of adjacent vertices to vi). The matrix L(G)=D(G) − A(G) is called the Laplacian matrix of graph G, where D(G)=diag(dv1, dv2,..., dvn ) denotes the diagonal matrix of vertex degrees of G.
Definition: A unicyclic molecular graph is a connected graph G containing exactly one cycle.
Unicyclic Molecular Graphs
In this section, we will give all unicyclic molecular graphs with at most 8 vertices.
Lemma
There are exactly 143 unicyclic molecular graphs with 3 ≤ n ≤ 8 vertices.
Proof. From [22, p. 213-215] one can find all unicyclic molecular graphs for 3 ≤ n ≤ 8, where n is the number of vertices in the unicyclic molecular graph G
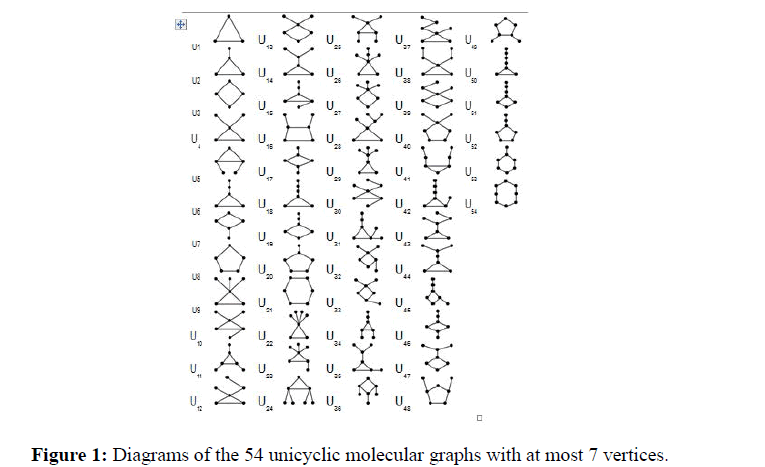
On (Figure 1), we give all the diagrams of the 54 unicyclic molecular graphs with at most 7 vertices. On (Figure 2), we give all the diagrams of the 89 unicyclic molecular graphs with exactly 8 vertices. We denote all these unicyclic molecular graphs by Ui for i=1,..., 143. Clearly, on (Figure 1), U1 is a cycle C3, U3 is a cycle C4, U8 is a cycle C5, U21 is a cycle C6 and U54 is a cycle C7. On Figure 2, U143 is a cycle C8.
Partial Proof Of The Conjecture
From, (Figure 1 and 2), we have all unicyclic molecular graphs Ui for i=1,..., 143 with at most 8 vertices. In the first column of the following tables (Tables 1-3), we give the name Ui for i=1,..., 143, in the second column the number of vertices n, in the third column the Laplacian spectrum and in the fourth column we give Laplacian energy-like invariant LEL. By direct calculation (one can do this exercise by computer, by use of suitable mathematical softwares, for example Matlab or athematica) we find the Laplacian spectrum of each unicyclic molecular graph Ui and the Laplacian energy-like invariant LEL.
Now, if n=3, then we have only one unicyclic molecular graph U1=C3, with LEL ≈ 3.4146, for n=4, U3=C4 has the maximal LEL among all unicyclic molecular graphs with 4 (Tables 1 and 2) vertices, for n=5, U8=C5 has the maximal LEL among all unicyclic molecular graphs with 5 (Table 3) vertices, for n=6, U21=C6 has the maximal LEL among all the unicyclic molecular graphs with 6 vertices, for n=7, U54=C7 has the maximal LEL among all unicyclic molecular graphs with 7 vertices and for n=8, U143=C8 has the maximal LEL among all unicyclic molecular graphs with 8 vertices. Consequently, we can see that the conjecture 1.1 is true for 3 ≤ n ≤ 8.
| # | n | Laplacian spectrum | LEL |
|---|---|---|---|
| U1 | 3 | 0, 3, 3 | 3.4641 |
| U2 | 4 | 0, 1, 3, 4 | 4.7321 |
| U3 | 4 | 0, 2, 2, 4 | 4.8284 |
| U4 | 5 | 0, 0.5188, 2.3111, 3, 4.1701 | 6.0146 |
| U5 | 5 | 0, 0.6972, 1.3820, 3.6180, 4.3028 | 5.987 |
| U6 | 5 | 0, 1, 1, 3, 5 | 5.9681 |
| U7 | 5 | 0, 0.8299, 2, 2.6889, 4.4812 | 6.0819 |
| U8 | 5 | 0, 1.3820, 1.3820, 3.6180, 3.6180 | 6.1554 |
| U9 | 6 | 0, 0.3249, 1.4608, 3, 3, 4.2143 | 7.2956 |
| U10 | 6 | 0, 0.6571, 1, 2.5293, 3, 4.8136 | 7.327 |
| U11 | 6 | 0, 0.7639, 1, 2, 3, 5.2361 | 7.3085 |
| U12 | 6 | 0, 0.4384, 1, 3, 3, 4.5616 | 7.262 |
| U13 | 6 | 0, 0.4859, 1, 2.4280, 3, 5.0861 | 7.2426 |
| U14 | 6 | 0, 1, 1, 1, 1, 3, 6 | 7.1815 |
| U15 | 6 | 0, 0.6314, 1, 1.4738, 3.7877, 5.1071 | 7.2147 |
| U16 | 6 | 0, 0.4131, 1.1369, 2.3595, 3.6977, 4.3928 | 7.2639 |
| U17 | 6 | 0, 0.6972, 0.6972, 2, 4.3028, 4.3028 | 7.2328 |
| U18 | 6 | 0, 0.4384, 2, 2, 3, 4.5616 | 7.3584 |
| U19 | 6 | 0, 0.5858, 1.2679, 2, 3.4142, 4.7321 | 7.3287 |
| U20 | 6 | 0, 0.6972, 1.3820, 2, 3.6180, 4.3028 | 7.4012 |
| U21 | 6 | 0, 1, 1, 3, 3, 4 | 7.4641 |
| U22 | 7 | 0, 1, 1, 1, 1, 3, 7 | 8.3778 |
| U23 | 7 | 0, 0.5961, 1, 1, 1.5196, 3.8273, 6.0570 | 8.4222 |
| U24 | 7 | 0, 0.5505, 1, 1, 1.5858, 4.4142, 5.4495 | 8.4367 |
| U25 | 7 | 0, 0.6086, 0.6972, 1, 2.2271, 4.3028, 5.1642 | 8.4543 |
| U26 | 7 | 0, 0.4659, 1, 1, 2.4827,3, 6.0514 | 8.4502 |
| U27 | 7 | 0, 0.7269, 1, 1, 2, 3.1404, 6.1326 | 8.5153 |
| U28 | 7 | 0, 0.3983, 1, 1, 3, 3.3399, 5.2618 | 8.4846 |
| U29 | 7 | 0, 0.3983, 1, 1, 3, 3.3399, 5.2618 | 8.4846 |
| U30 | 7 | 0, 0.4116, 0.7530, 1.4064, 2.4450, 3.8019, 5.1819 | 8.4851 |
| U31 | 7 | 0, 0.3679, 1, 1.1879, 2.3732, 3.9464, 5.1228 | 8.4869 |
| U32 | 7 | 0, 0.5858, 1, 1, 2.5858, 3.4142, 5.4142 | 8.548 |
| U33 | 7 | 0, 0.5140, 1, 1.3364, 2, 3.8360, 5.3136 | 8.5514 |
| U34 | 7 | 0, 0.3820, 0.6972, 1.5858, 2.6180, 4.3028, 4.4142 | 8.5057 |
| U35 | 7 | 0, 0.3403, 1, 1.1451, 3, 3.8549, 4.6567 | 8.5075 |
| U36 | 7 | 0, 0.5858, 0.6837, 1.4206, 2.8654, 3.4142, 5.0303 | 8.5675 |
| U37 | 7 | 0, 0.2955, 1, 1.4911, 3, 3.1169, 5.09665 | 8.5198 |
| U38 | 7 | 0, 0.3820, 0.6086, 2.2271, 2.6180, 3, 5.1642 | 8.5131 |
| U39 | 7 | 0, 0.4330, 0.8510, 2, 2.3024, 3.1129, 5.3006 | 8.5787 |
| U40 | 7 | 0, 0.6086, 1, 1.3820, 2.2271, 3.6180, 5.1642 | 8.6227 |
| U41 | 7 | 0, 0.3004, 0.7530, 2.2391, 2.4450, 3.8019, 4.4605 | 8.5377 |
| U42 | 7 | 0, 0.2679, 1, 1.5858, 3, 3.7321, 4.4142 | 8.5418 |
| U43 | 7 | 0, 0.3217, 0.6802, 2.1397, 3, 3.2297, 4.6287 | 8.5353 |
| U44 | 7 | 0, 0.2679, 1, 1.5858, 3, 3.7321, 4.4142 | 8.5418 |
| U45 | 7 | 0, 0.3820, 0.8851, 2, 2.6180, 3.2541, 4.8608 | 8.5997 |
| U46 | 7 | 0, 0.3588, 1, 2, 2.2763, 3.5892, 4.7757 | 8.6018 |
| U47 | 7 | 0, 0.3588, 1, 2, 2.2763, 3.5892, 4.7757 | 8.6018 |
| U48 | 7 | 0, 0.5188, 1, 1.5858, 2.3111, 4.1701, 4.4142 | 8.6429 |
| 6 |
Table 1: Partial proof of the conjecture.
| # | n | Laplacian spectrum | LEL |
|---|---|---|---|
| U49 | 7 | 0, 0.6228, 0.7530, 1.7261, 2.4450, 3.8019, 4.6511 | 8.6409 |
| U50 | 7 | 0, 0.2254, 1, 2.1859, 3, 3.3604, 4.2283 | 8.5747 |
| U51 | 7 | 0, 0.2765, 1.3323, 2, 2.5219, 3.2920, 4.5772 | 8.6362 |
| U52 | 7 | 0, 0.3820, 1.3820, 1.5858 ,2.6180, 3.6180, 4.4142 | 8.6741 |
| U53 | 7 | 0, 0.5858, 1, 1.5858, 3, 3.4142, 4.4142 | 8.7055 |
| U54 | 7 | 0, 0.7530, 0.7530, 2.4450, 2.4450, 3.8019, 3.8019 | 8.7625 |
| U55 | 8 | 0, 1, 1, 1, 1, 1, 3, 8 | 9.5605 |
| U56 | 8 | 0, 1, 1, 1, 1.5468, 7.0362 | 9.6142 |
| U57 | 8 | 0, 0.5069, 1, 1, 1, 1.6400, 4.6654, 6.1877 | 9.6401 |
| U58 | 8 | 0, 0.5607, 0.9672, 1, 1, 2.3389, 4.3028, 6.1004 | 9.6573 |
| U59 | 8 | 0, 0.5505, 0.6571, 1, 1, 2.5293, 4.8136, 5.4495 | 9.9714 |
| U60 | 8 | 0, 0.7029, 1, 1, 1, 2, 3.2132, 7.0839 | 9.7067 |
| U61 | 8 | 0, 0.4592, 1, 1, 1, 2.5135, 3, 7.0340 | 9.6423 |
| U62 | 8 | 0, 0.3738, 1, 1, 1, 3, 3.4849, 6.1413 | 9.6884 |
| U63 | 8 | 0, 0.5449, 1, 1, 1, 2.5987, 3.6291, 6.2273 | 9.7507 |
| U64 | 8 | 0, 0.4746, 1, 1, 1.3691, 2, 4, 6.1563 | 9.7544 |
| U65 | 8 | 0, 0.3738, 1, 1, 1, 3, 3.4849, 6.1413 | 9.6884 |
| U66 | 8 | 0, 0.3417, 1, 1, 1.2176, 2.3795, 4, 6.0612 | 9.6925 |
| U67 | 8 | 0, 0.4103, 0.6758, 1, 1.4853, 2.4907, 3.8322, 6.1057 | 9.6881 |
| U68 | 8 | 0, 0.3542, 1, 1, 1, 3, 4, 5.6458 | 9.7033 |
| U69 | 8 | 0, 0.5107, 1, 1, 1, 2.7108, 4, 5.7785 | 9.7649 |
| U70 | 8 | 0, 0.4384, 1, 1, 1.4384, 2, 4.5616, 5.5616 | 9.7698 |
| U71 | 8 | 0, 0.3676, 0.7223, 1, 1.5047, 2.4500, 4.4669, 5.4885 | 9.7044 |
| U72 | 8 | 0, 0.3568, 0.6365, 1, 1.6887, 2.7571, 4.3873, 5.1735 | 9.7242 |
| U73 | 8 | 0, 0.5858, 0.5858, 1, 1.4384, 3.4142, 3.4142, 5.5616 | 9.7839 |
| U74 | 8 | 0, 0.5066, 0.6743, 1, 1.4986, 2.8999, 3.9168, 5.5038 | 9.7851 |
| U75 | 8 | 0, 0.3339, 0.7460, 1, 1.4123, 3.3136, 3.8587, 5.3356 | 9.7245 |
| U76 | 8 | 0, 0.3030, 1, 1, 1.1479, 3.2427, 4, 5.2863 | 9.7218 |
| U77 | 8 | 0, 0.2967, 1, 1, 1.2048, 3, 4.3310, 5.1675 | 9.7287 |
| U78 | 8 | 0, 0.3820, 0.6972, 0.7639, 2, 2.6180, 4.3028, 5.2361 | 9.7219 |
| U79 | 8 | 0, 0.3065, 0.6972, 1, 1.6703, 3.3297, 4.3028, 4.6935 | 9.7465 |
| U80 | 8 | 0, 0.5858, 0.5858, 0.7639, 2, 3.4142, 3.4142, 5.2361 | 9.8027 |
| U81 | 8 | 0, 0.3820, 0.5607, 1, 2.3389, 2.6180, 3, 6.1004 | 9.7162 |
| U82 | 8 | 0, 0.5607, 1, 1, 1.3820, 2.3389, 3.6180, 6.1004 | 9.8257 |
| U83 | 8 | 0, 0.4284, 0.7828, 1, 2, 2.4204, 3.1905, 6.1779 | 9.781 |
| U84 | 8 | 0, 0.2774, 1, 1, 1.5068, 3, 3.1610, 6.0548 | 9.7248 |
| U85 | 8 | 0, 0.2888, 0.6742, 1, 2.1694, 3, 3.5857, 5.2819 | 9.7553 |
| U86 | 8 | 0, 0.5447, 0.7347, 1, 1.7635, 2.7242, 3.9063, 5.3266 | 9.858 |
| U87 | 8 | 0, 0.4484, 1, 1, 1.6280, 2.4815, 4.2659, 5.1762 | 9.8614 |
| U88 | 8 | 0, 0.3479, 0.8495, 1, 2, 2.7627, 3.6076, 5.4323 | 9.818 |
| U89 | 8 | 0, 0.3187, 1, 1, 2, 2.3579, 4, 5.3234 | 9.8215 |
| U90 | 8 | 0, 0.3820, 0.7254, 1, 2.3000, 2.6180, 3.5096, 5.4651 | 8.5418 |
| U91 | 8 | 0, 0.3581, 0.6918, 1.2843, 2, 2.4091, 3.8877, 5.3689 | 9.8186 |
| U91 | 8 | 0, 0.3479, 0.8495, 1, 2, 2.7627, 3.6076, 5.4323 | 9.818 |
| U93 | 8 | 0, 0.3187, 1, 1, 2, 2.3579, 4, 5.3234 | 9.8215 |
| U94 | 8 | 0, 0.3187, 0.5858, 1, 2.3579, 3, 3.4142, 5.3234 | 9.7525 |
| U95 | 8 | 0, 0.2384, 1, 1, 1.6367, 3, 4, 5.1249 | 9.7635 |
| U96 | 8 | 0, 0.2955, 0.5979, 1449, 2.3295, 2.4734, 3.9635, 5.1952 | 9.756 |
| 7 |
Table 2 : Partial proof of the conjecture.
| # | n | Laplacian spectrum | LEL | |
|---|---|---|---|---|
| U97 | 8 | 0, 0.3187, 0.5858, 1, 2.3579, 3, 3.4142, 5.3234 | 9.7525 | |
| U98 | 8 | 0, 0.2384, 1, 1, 1.6367, 3, 4, 5.1249 | 9.7635 | |
| U99 | 8 | 0, 0.2593, 0.7150, 1.3232, 1.5891, 3.1143, 3.8086, 5.1905 | 9.7603 | |
| U100 | 8 | 0, 0.3820, 0.4280, 1.2285 ,2.2799, 2.6180, 3.8123, 5.2513 | 9.7527 | |
| U101 | 8 | 0, 0.2384, 1, 1, 1.6367, 3, 4, 5.1249 | 9.7635 | |
| U102 | 8 | 0, 0.3004, 0.4915, 1.3204, 2.2391, 2.8258, 4.3623, 4.4605 | 9.7762 | |
| U103 | 8 | 0, 0.5188, 0.6571, 1, 2.3111, 2.5293, 4.1701, | 4.8136 | 9.8776 |
| U104 | 8 | 0, 0.4915, 0.6228, 1.3204, 1.7261, 2.8258, 4.3623, 4.6511 | 9.8794 | |
| U105 | 8 | 0, 0.3074, 0.8828, 1, 2.2699, 2.7125, 3.8417, | 4.9857 | 9.8405 |
| U106 | 8 | 0, 0.2907, 1, 1, 2, 2.8061, 4, 4.9032 | 9.8428 | |
| U107 | 8 | 0, 0.3636, 0.5858, 1.3478, 2, 3.2222, 3.4142, | 5.0664 | 9.8372 |
| U108 | 8 | 0, 0.3432, 0.6639, 1.1805, 2.2491, 2.9045, 3.5994, 5.0594 | 9.8376 | |
| U109 | 8 | 0, 0.2679, 0.6571, 1, 2.5293, 3, 3.7321, 4.8136 | 9.7765 | |
| U110 | 8 | 0, 0.2588, 0.6436, 1.1385, 2.1603, 3.1943, 3.8943, 4.7103 | 9.7788 | |
| U111 | 8 | 0, 0.2183, 1, 1, 1.7127, 3.5524, 4, 4.5166 | 9.7859 | |
| U112 | 8 | 0, 0.2509, 0.7287, 1, 2.3349, 3, 4, 4.6855 | 9.7792 | |
| U113 | 8 | 0, 0.2434, 0.6972, 1.1798, 2, 3.1386, 4.3028, | 4.4383 | 9.7814 |
| U114 | 8 | 0, 0.2023, 1, 1, 2.2472, 3, 3.4527, 5.0979 | 9.7969 | |
| U115 | 8 | 0, 0.4965, 1, 1, 1.7356, 3, 3.5767, 5.1912 | 9.9237 | |
| U116 | 8 | 0, 0.3820, 0.7639, 1.3820, 2, 2.6180, 3.6180, | 5.2361 | 9.8903 |
| U117 | 8 | 0, 0.2652, 0.8350, 1.4524, 2, 2.8415, 3.2984, | 5.3075 | 9.8538 |
| U118 | 8 | 0, 0.3820, 0.4711, 2, 2, 2.6180, 3.1674, 5.3615 | 9.8461 | |
| U119 | 8 | 0, 0.2538, 0.5472, 1.4689, 2.4066, 3, 3.1504, | 5.1732 | 9.7883 |
| U120 | 8 | 0, 0.5858, 0.5858, 1.2679, 2, 3.4142, 3.4142, | 4.7321 | 9.9418 |
| U121 | 8 | 0, 0.4679, 0.7369, 1.4843, 1.6527, 3.1826, 3.8794, 4.5962 | 9.9438 | |
| U122 | 8 | 0, 0.4384, 1, 1, 2, 3, 4, 4.5616 | 9.9442 | |
| U123 | 8 | 0, 0.3095, 1, 1.3820, 1.6703, 3.3297, 3.6180, | 4.6935 | 9.9149 |
| U124 | 8 | 0, 0.3547, 0.7089, 1.5498, 2, 2.8407, 3.8349, | 4.711 | 9.9109 |
| U125 | 8 | 0, 0.3249, 0.8299, 1.4608, 2, 2.6889, 4.2143, | 4.4812 | 9.9134 |
| U126 | 8 | 0, 0.2679, 0.6571, 2, 2, 2.5293, 3.7321, 4.8136 | 9.8729 | |
| U127 | 8 | 0, 0.2243, 1, 1.4108, 2, 2.7237, 4, 4.6412 | 9.8803 | |
| U128 | 8 | 0, 0.2442, 0.8455, 1.3465, 2.4678, 2.7742, 3.4537, 4.8681 | 9.8754 | |
| U129 | 8 | 0, 0.2355, 0.8711, 1.5254, 2, 2.9050, 3.6799, | 4.7831 | 9.8776 |
| U130 | 8 | 0, 0.2907, 0.5858, 2, 2, 2.8061, 3.4142, 4.9032 | 9.8702 | |
| U131 | 8 | 0, 0.2679, 0.6571, 2, 2, 2.5293, 3.7321, 4.8136 | 9.8729 | |
| U132 | 8 | 0, 0.2243, 0.5858, 1.4108, 2.7273, 3, 3.4142, | 4.6412 | 9.8113 |
| U133 | 8 | 0, 0.3065, 0.3820, 1.6703, 2.6180, 3, 3.3297, | 4.6935 | 9.8054 |
| U134 | 8 | 0, 0.2137, 0.6177, 1.4977, 2.3537, 3, 3.8408, | 4.4763 | 9.8138 |
| U135 | 8 | 0, 0.1864, 1, 1, 2.4707, 3, 4, 4.3429 | 9.8196 | |
| U136 | 8 | 0, 0.1892, 0.8207, 1.2558, 2.2216, 3.3354, 3.7575, 4.4198 | 9.8191 | |
| U137 | 8 | 0, 0.2137, 0,6177, 1.4977, 2.3537, 3, 3.8408, | 4.4763 | 9.8138 |
| U138 | 8 | 0, 0.4915, 0.7530, 1.3204, 1.4450, 2.8258, 3.8019, 4.3623 | 10.001 | |
| U139 | 8 | 0, 0.3376, 1, 1.2426, 2.4249, 3, 3.4959, 4.4989 | 9.9758 | |
| U140 | 8 | 0, 0.2434, 1.1798, 1.3820, 2, 3.1386, 3.6180, | 4.4383 | 9.9498 |
| U141 | 8 | 0, 0.1930, 0.9231, 2, 2, 2.7890, 3.5143, 4.5806 | 9.9134 | |
| U142 | 8 | 0, 0.1667, 0.7276, 1.6353, 2.6729, 3, 3.5643, | 4.2332 | 9.8524 |
| U143 | 8 | 0, 0.5858, 0.5858, 2, 2, 3.4142, 3.4142, | 4 | 10.0547 |
Table 3 : Partial proof of the conjecture.
On the other hand from (Tables 4-6), we can easily see that the energy E of U3=C4, U8=C5, U21=C6 and U54=C7 is maximal among all other unicyclic molecular graphs in the same number of vertices. But for n=8 the unicyclic molecular graph U143=C8 has energy 9.6568 which is less then energy of U140 and U142. Hence among the unicyclic molecular graphs the cycle Cn has maximal energy E for 3 ≤ n ≤ 7 but for n=8 it is not true.
| # | n | Adjacency spectrum | E |
|---|---|---|---|
| U1 | 3 | 2, 1, 1 | 4 |
| U2 | 4 | 2.1701, 0.3111, 1:0000, 1:4812 | 4.9624 |
| U3 | 4 | 2, 0, 0, 2 | 4 |
| U4 | 5 | 2.3429, 0.4707, 0, 1:0000, 1:8136 | 5.6272 |
| U5 | 5 | 2.3028, 0.6180, 0, 1:3028, 1:6180 | 5.8416 |
| U6 | 5 | 2.2143, 1.0000, 0:5392, 1:0000, 1:6751 | 6.4286 |
| U7 | 5 | 2.1358, 0.6622, 0, 0:6622, 2:1358 | 5.5959 |
| U8 | 5 | 2, 0.6180, 0.6180, 1:6180, 1:6180 | 6.4721 |
| U9 | 6 | 2.5141, 0.5720, 0, 0, 1, 2:0861 | 6.1723 |
| U10 | 6 | 2.4458, 0.7968, 0, 0, 1:3703, 1:8723 | 6.4852 |
| U11 | 6 | 2.4142, 0.6180, 0.6180, 0:4142, 1:6180, 1:6180 | 7.3006 |
| U12 | 6 | 2.3799, 1, 0.2914, 0:7510, 1, -1.9202 | 7.3725 |
| U13 | 6 | 2.2882, 0.8740, 0, 0, 0:8740, 2:2882 | 6.3246 |
| U14 | 6 | 2.2784, 1.3174, 0, 0:7046, 1, 1:8912 | 7.1917 |
| U15 | 6 | 2.3342, 1.0996, 0.2742, 5945, 1:3738, 1:7397 | 7.416 |
| U16 | 6 | 2.2470, 0.8019, 0.5550, 0:5550, 0:8019, 2:2470 | 7.2078 |
| U17 | 6 | 2.2361, 1, 0, 0, 1, 2:2361 | 6.4721 |
| U18 | 6 | 2.2283, 1.3604, 0.1859, 1, 1, 1:7746 | 7.5492 |
| U19 | 6 | 2.1753, 1.1260, 0, 0, 1:1260, 2:1753 | 6.6027 |
| U20 | 6 | 2.1149, 1, 0.6180, 0:2541, 1:6180, 1:8608 | 7.4659 |
| U21 | 6 | 2, 1, 1, 1, 1, 2 | 8 |
| U22 | 7 | 2.6113, 0.6421, 0, 0, 0, 1, 2:3234 | 6.6468 |
| U23 | 7 | 2.5944, 0.9159, 0, 0, 0, 1:3883, 2:1220 | 7.0206 |
| U24 | 7 | 2.5616, 1, 0, 0, 0, 1:5616, 2 | 7.1231 |
| U25 | 7 | 2.5374, 0.8493, 0.6180, 0, 04891, 1:6180, 1:8976 | 8.0095 |
| U26 | 7 | 2.5450, 1, 0.4394, 0, 0:8302, 1, 2:1542 | 7.9688 |
| U27 | 7 | 2.4495, 1, 0, 0, 0, 1, 2:4495 | 6.899 |
| U28 | 7 | 2.4309, 1.3269, 0.3011, 0, 1, 1, 2:0590 | 8.1179 |
| U29 | 7 | 2.6368, 1.5262, 0, 0, 0:7877, 1, 2:1071 | 7.7896 |
| U30 | 7 | 2.4745, 1.1143, 0.5241, 0, 0:7615, 1:3891, 1:9624 | 8.2259 |
| U31 | 7 | 2.4676, 1.1883, 0.3867, 0, 0:6043, 1:5274, 1:9108 | 8.0851 |
| U32 | 7 | 2.3761, 1, 0.5952, 0, 0:5952, 1, 2:3761 | 7.9425 |
| U33 | 7 | 2.3583, 1.1994, 0, 0, 0, 1:1994, 2:3583 | 7.1153 |
| U34 | 7 | 2.4383, 1.1386, 0.6180, 0, 0:8202, 1:6180, 1:7566 | 8.3898 |
| U35 | 7 | 2.3799, 1.4142, 0.2914, 0, 0:7510, 1:4142, 1:9202 | 8.1709 |
| U36 | 7 | 2.3344, 1, 0.7420, 0, 0:7420, 1, 2:3344 | 8.1528 |
| U37 | 7 | 2.3894, 1.3668, 0.3944, 0, 1, 1:1852, 1:9653 | 8.3011 |
| U38 | 7 | 2.4142, 1, 1, 0:4142, 1, 1, 2 | 8.8284 |
| U39 | 7 | 2.3244, 1.1472, 0.5304, 0, 0:5304, 1:1472, 2:3244 | 8.0038 |
| U40 | 7 | 2.2562, 1.1899, 0.6180, 0, 0:3565, 1:6180, 2:0896 | 8.1283 |
| U41 | 7 | 2.3623, 1.2470, 0.8258, 0:4450, 0:6796, 1:5085, 1:8019 | 8.8702 |
| U42 | 7 | 2.3429, 1.4142, 0.4707, 0, 1, 1:4142, 1:8136 | 8.4556 |
| U43 | 7 | 2.2970, 1.4933, 0.6400, 0:4631, 1, 1, 1:9672 | 8.8606 |
| U44 | 7 | 2.2533, 1.6449, 0.2327, 0, 1, 1:2033, 1:9275 | 8.2616 |
| U45 | 7 | 2.2764, 1.1859, 0.6416, 0, 0:6416, 1:1859, 2:2764 | 8.2078 |
| U46 | 7 | 2.2638, 1.2793, 0.4883, 0, 0:4883, 1:2793, 2:2638 | 8.0629 |
| U47 | 7 | 2.2361, 1.4142, 0, 0, 0, 1:4142, 2:2361 | 7.3006 |
| U48 | 7 | 2.1987, 1.2470, 0.7135, 0, 0:4450, 1:8019, 1:9122 | 8.3184 |
| 9 |
Table 4: Partial proof of the conjecture.
| # | n | Adjacency spectrum | E |
|---|---|---|---|
| U49 | 7 | 2.2143, 1, 1, 0, 0:5392, 1:6751, 2 | 8.4286 |
| U50 | 7 | 2.2332, 1.5643, 0.6729, 0:3647, 1, 1:2724, -1.8333 | 8.9408 |
| U51 | 7 | 2.1889, 1.4142, 0.4569, 0, 0:4569, 1:4142, 2:1889 | 8.1199 |
| U52 | 7 | 2.1515, 1.2685, 0.6180, 0.4206 , 0:8958, 1:6180, 1:9449 | 8.9174 |
| U53 | 7 | 2.1010, 1.2593, 1, 0, 1, 1:2593, 2:1010 | 8.7206 |
| U54 | 7 | 2, 1.2470, 1.2470, 0:4450, 0:4450, 1:8019, 1:8019 | 8.9879 |
| U55 | 8 | 2.8434, 0.6932, 0, 0, 0, 0, 1, 2:5366 | 7.0732 |
| U56 | 8 | 2.7448, 1, 0, 0, 0, 0, 1:3959, 2:3489 | 7.4896 |
| U57 | 8 | 2.6872, 1.1408, 0, 0, 0, 0, 1:6396, 2:1885 | 7.6561 |
| U58 | 8 | 2.6691, 1, 0.6180, 0, 0, 0:5240, 1:6180, 2:1451 | 8.5742 |
| U59 | 8 | 2.6412, 1, 0.7237, 0, 0, 0:5892, 1:7757, 2 | 8.27298 |
| U60 | 8 | 2.6131, 1.0824, 0, 0, 0, 0, 1:0824, 2:6131 | 7.391 |
| U61 | 8 | 2.7073, 1, 0.5359, 0, 0, 0:8719, 1, 2:3713 | 8.4864 |
| U62 | 8 | 2.4860, 1.6636, 0, 0, 0, 0:8360, 1, 2:3136 | 8.2992 |
| U63 | 8 | 2.5178, 1.1380, 0.6045, 0, 0, 0:6045, 1:1380, 2:5178 | 8.5206 |
| U64 | 8 | 2.4972, 1.3281, 0, 0, 0, 0, 1:3281, 2:4972 | 7.6506 |
| U65 | 8 | 2.5860, 1.3350, 0.4559, 0, 0, 1, 1:1317, 2:2453 | 8.7539 |
| U66 | 8 | 2.6095, 1.2598, 0.4468, 0, 0, 0:6084, 1:5710, 2:1367 | 8.6322 |
| U67 | 8 | 2.6200, 1.1311, 0.6634, 0, 0, 0:8339, 1:3962, 2:1843 | 8.8289 |
| U68 | 8 | 2.5009, 1.5558, 0.3044, 0, 0, 1, 1:1401, 2:2208 | 8.7223 |
| U69 | 8 | 2.4812, 1.1701, 0.6889, 0, 0, 0:6889, 1:1701, 2:4812 | 8.6804 |
| U70 | 8 | 2.4495, 1.4142, 0, 0, 0, 0, 1:4142, 2:4495 | 7.7274 |
| U71 | 8 | 2.5831, 1.2346, 0.6180, 0, 0, 0:7631, 1:6180, 2:0545 | 8.8713 |
| U72 | 8 | 2.5553, 1.1946, 0.7799, 0, 0, 0:8911, 1:7177, 1:9210 | 9.0596 |
| U73 | 8 | 2.4495, 1, 1, 0, 0, 1, 1, 2:4495 | 8.899 |
| U74 | 8 | 2.4412, 1.2124, 0.7555, 0, 0, 0:7555, 1:2124, 2:4412 | 88,182 |
| U75 | 8 | 2.5141, 1.4142, 0.5720, 0, 0, 1, 1:4142, 2:0861 | 9.0006 |
| U76 | 8 | 2.4465, 1.6383, 0.2976, 0, 0, 0:8262, 1:4347, 2:1216 | 8.7649 |
| U77 | 8 | 2.4989, 1.4959, 0.4249, 0, 0, 0:7574, 1:6624, 2 | 8.8395 |
| U78 | 8 | 2.5606, 1.1676, 0.6180, 0.5038, 0:3905, 0:8565, 1:6180, 1:9850 | 9.7 |
| U79 | 8 | 2.4728, 1.4626, 0.6180, 0, 0, 1, 1:6180, 1:9354 | 9.1068 |
| U80 | 8 | 2.4142, 1, 1, 0.4142, 0:4142, 1, 1, 2:4142 | 9.6568 |
| U81 | 8 | 2.5714, 1, 1, 0.2754, 0:6379, 1, 1, 2:2116 | 9.699 |
| U82 | 8 | 2.4142, 1.3028, 0.6180, 0, 0, 0:4142, 1:6180, 2:3028 | 8.67 |
| U83 | 8 | 2.4812, 1.1701, 0.6889, 0, 0, 0:6889, 1:1701, 2:4812 | 8.6804 |
| U84 | 8 | 2.5516, 1.3720, 0.5185, 0, 0, 1, 1:2658, 2:1762 | 8.8841 |
| U85 | 8 | 2.4433, 1.5115, 0.6465, 0.2894, 0:5614, 1, 1:2249, 2:1044 | 9.7814 |
| U86 | 8 | 2.3371, 1.2089, 1, 0, 0, 0:6699, 1:6975, 2:1786 | 9.092 |
| U87 | 8 | 2.3113, 1.4269, 0.7353, 0, 0, 0:5338, 1:8365, 2:1032 | 8.947 |
| U88 | 8 | 2.3761, 1.4142, 0.5952, 0, 0, 0:5952, 1:4142, 2:3761 | 8.771 |
| U89 | 8 | 2.3268, 1.6080, 0, 0, 0, 0, 1:6080, 2:3268 | 7.8696 |
| U90 | 8 | 2.4049, 1.2293, 0.6728, 0.5027, 0:5027, 0:6728, 1:2293, 2:4049 | 9.6194 |
| U91 | 8 | 2.3867, 1.3497, 0.6941, 0, 0, 0:6941, 1:3497, 2:3867 | 8.861 |
| U92 | 8 | 2.3968, 1.2665, 0.8069, 0, 0, 0:8069, 1:2665, 2:3968 | 8.9404 |
| U93 | 8 | 2.3761, 1.4142, 0.5952, 0, 0, 0:5952, 1:4142, 2:4161 | 8.771 |
| U94 | 8 | 2.4615, 0.3370, 1, 0, 0:4750, 1, 1:2118, 2:1118 | 9.5971 |
| U95 | 8 | 2.4048, 1.6628, 0.4231, 0, 0, 1, 1:4446, 2:0461 | 8.9814 |
| U96 | 8 | 2.4943, 1.2898, 0.8539, 0.2621, 0:5812, 0:7701, 1:5625, 1:9863 | 9.8002 |
| 10 |
Table 5 : Partial proof of the conjecture.
| # | n | Adjacency spectrum | E |
|---|---|---|---|
| U97 | 8 | 2.3914, 1.6180, 0.7729, 0, 0:6180, 1, 1, 2:1642 | 9.5645 |
| U98 | 8 | 2.3028, 1.8608, 0.2541, 0, 0, 1, 1:3028, 2:1149 | 6.134722 |
| U99 | 8 | 2.4812, 1.4142, 0.6889, 0, 0, 1:1701, 1:4142, 2 | 9.1686 |
| U100 | 8 | 2.5019, 1.1643, 1, 0.2493, 0:4848, 1, 1:3965, 2:0341 | 9.8309 |
| U101 | 8 | 2.4728, 1.4626, 0.6180, 0, 0, 1, 1:6180, 1:9354 | 9.1068 |
| U102 | 8 | 2.4605, 1.2470, 1, 0.2391, 0:4450, 1, 1:6996, 1:8019 | 9.8931 |
| U103 | 8 | 2.2904, 1.2470, 1, 0.3620, 0:4450, 0:5828, 1:8019, 2:0696 | 9.7987 |
| U104 | 8 | 2.2784, 1.3174, 1, 0, 0, 0:7046, 1:8912, 2 | 9.1916 |
| U105 | 8 | 2.3213, 1.4789, 0.6513, 0, 0, 0:6513, 1:4789, 2:3213 | 8.903 |
| U106 | 8 | 2.3072, 1.5355, 0.5645, 0, 0, 0:5645, 1:5355, 2:3072 | 8.8144 |
| U107 | 8 | 2.3583, 1.1993, 1, 0, 0, 1, 1:1993, 2:3583 | 9.1152 |
| U108 | 8 | 2.3562, 1.2918, 0.7741, 0.4244, 0:4244, 0:7741, 1:2918, 2:3562 | 9.693 |
| U109 | 8 | 2.3278, 1.6942, 0.7897, 0, 0:5017, 1, 1:2320, 2:0779 | 9.6233 |
| U110 | 8 | 2.3920, 1.5739, 0.6852, 0.2715, 0:5010, 1, 1:4339, 1:9877 | 9.8452 |
| U111 | 8 | 2.3577, 1.6931, 0.5273, 0, 0, 1:1628, 1:4708, -1.9445 | 9.1562 |
| U112 | 8 | 2.4035, 1.4835, 0.9277, 0, 0:5022, 0:7790, 1:5934, 1:9401 | 9.6294 |
| U113 | 8 | 2.4442, 1.4421, 0.6180, 0.4165, 0:3239, 1:1497, 1:6180, 1:8292 | 9.8416 |
| U114 | 8 | 2.3920, 1.5739, 0.6852, 0.2715, 0:5010, 1, 1:4339, 1:9877 | 9.8452 |
| U115 | 8 | 2.2361, 1.4142, 1, 0, 0, 1, 1:4142, 2:2361 | 9.3006 |
| U116 | 8 | 2.2922, 1.3281, 0.6852, 0.6180, 0:2448, 0:9109, 1:6180, 2:1500 | 9.8472 |
| U117 | 8 | 2.3344, 1.4142, 0.7420, 0, 0, 0:7420, 1:4142, 2:3344 | 8.9812 |
| U118 | 8 | 2.3583, 1.1993, 1, 0, 0, 1, 1:1993, 2:3583 | 9.1152 |
| U119 | 8 | 2.4227, 1.3726, 1, 0.1765, 0:6500, 1, 1:2897, 2:0321 | 9.9436 |
| U120 | 8 | 2.1935, 1.2950, 1.1935, 0.2950, 0:2950, 1:1935, 1:2950, 2:1935 | 9.954 |
| U121 | 8 | 2.1753, 1.4142, 1.1260, 0, 0, 1:1260, 1:4142, 2:1753 | 9.431 |
| U122 | 8 | 2.1701, 1.4812, 1, 0.3111, 0:3111, 1, 1:4812, 2:1701 | 9.9248 |
| U123 | 8 | 2.2105, 1.5047, 0.6180, 0.5043, 0, 1:1554, 1:6180, 2:0641 | 9.675 |
| U124 | 8 | 2.2427, 1.2858, 1, 0.4410, 0:2266, 1, 1:6895, 2:0534 | 9.939 |
| U125 | 8 | 2.2245, 1.4232, 0.8060, 0.5013, 0:2353, 0:9230, 1:8266, 1:9701 | 9.91 |
| U126 | 8 | 2.2552, 1.5582, 0.6970, 0, 0, 0:6970, 1:5582, 2:2552 | 9.0208 |
| U127 | 8 | 2.2143, 1.6751, 0.5392, 0, 0, 0:5392, 1:6751, 2:2143 | 8.8572 |
| U128 | 8 | 2.2853, 1.4534, 0.6880, 0.4376, 0:4376, 0:6880, 0:4534, 2:2853 | 9.7286 |
| U129 | 8 | 2.2725, 1.4924, 0.7801, 0, 0, 0:7801, 1:4924, 2:2725 | 9.09 |
| U130 | 8 | 2.3028, 1.3028, 1, 0, 0, 1, 1:3028, 2:3028 | 9.2112 |
| U131 | 8 | 2.2882, 1.4142, 0.8740, 0, 0, 0:8740, 1:4142, 2:2882 | 9.1528 |
| U132 | 8 | 2.3028, 1.6180, 1, 0, 0:6180, 1, 1:3028, 2 | 9.8416 |
| U133 | 8 | 2.3163, 1.5794, 1, 0.1346, 1, 1, 1, 2:0303 | 10.0606 |
| U134 | 8 | 2.2623, 1.7571, 0.7790, 0.1832, 0:6696, 1, 1:3234, 1:9886 | 9.9632 |
| U135 | 8 | 2.2429, 1.7928, 0.8048, 0, 0:4354, 1, 1:4573, 1:9478 | 9.681 |
| U136 | 8 | 2.3455, 1.5988, 0.7784, 0.2449, 0:4197, 1:2246, 1:4638, 1:8596 | 9.9353 |
| U137 | 8 | 2.3699, 1.4576, 1, 0.1724, 0:5771, 1, 1:5734, 1:8494 | 9.9998 |
| U138 | 8 | 2.0912, 1.4427, 1.2470, 0.2163, 0:4450, 0:7764, 1:8019, 1:9738 | 9.9943 |
| U139 | 8 | 2.1358, 1.4142, 1, 1.6621, 0:6621, 1, 1:4142, 2:1358 | 10.4242 |
| U140 | 8 | 2.1648, 1.4739, 0.7691, 0.6180, 0:1627, 1:2635, 1:6180, 1:9815 | 10.0515 |
| U141 | 8 | 2.1940, 1.5904, 0.8106, 0, 0, 0:8106, 1:5904, 2:1940 | 9.19 |
| U142 | 8 | 2.2350, 1.6881, 1, 0.1326, 0:7386, 1, 1:4460, 1:8711 | 10.1114 |
| U143 | 8 | 2, 1.4142, 1.4142, 0, 0, 1:4142, 1:4142, 2 | 9.6568 |
Table 6: Partial proof of the conjecture.
Conclusion
In this paper, our attention was focused on the Laplacian-energy-like invariant and energy of unicyclic molecular graphs with at most n vertices, where 3 ≤ n ≤ 8, and on the partial proof of the Conjecture 1.1. We have shown that Laplacian- energy-like invariant of cycle Cn is maximal among all other unicyclic molecular graphs for 3 ≤ n ≤ 8, a step towards the proof of the Conjecture 1.1.
References
- Gutman I (2005) Topology and stability of conjugated hydrocarbons: The dependence of total π-electron energy on molecular topology. J Serbian Chem Society 70: 441-456.
- Perić M, Gutman I, Radić-Perić J (2006) The Hückel total π-electron energy puzzle. Journal of the Serbian Chemical Society 71: 771-783.
- Gutman I (1992) Total π-electron energy of benzenoid hydrocarbons. In Advances in the Theory of Benzenoid Hydrocarbons II. Springer, Berlin, Heidelberg 29-63.
- Graovac A, Gotman I, Trinajstic N (2012) Topological approach to the chemistry of conjugated molecules (Vol. 4). Springer Science & Business Media.
- Gutman I, Polansky OE (1986) Automorphism Groups. In Mathematical Concepts in Organic Chemistry (pp. 108-116). Springer, Berlin, Heidelberg.
- Gutman I (2006) Chemical graph theory—The mathematical connection. Advances in Quantum Chemistry, 51, pp.125-138.
- Lin W, Guo X, Li H (2005). On the extremal energies of trees with a given maximum degree. MATCH Commun. Math. Comput. Chem, 54: 363-378.
- Li F, Zhou B (2005). Minimal energy of bipartite unicyclic graphs of a given bipartition. MATCH Commun. Math. Comput. Chem, 54 : 379-388.
- Yu A, Lu M, Tian F (2005) New upper bounds for the energy of graphs. MATCH Commun. Math. Comput. Chem, 53: 441-448.
- Yan W, Ye L (2005). On the maximal energy and the Hosoya index of a type of trees with many pendant vertices. MATCH Commun. Math. Comput. Chem, 53: 449-459.
- Indulal G, Vijayakumar A (2006) On a pair of equienergetic graphs. MATCH Commun. Math. Comput. Chem, 55: 83-90.
- Zhou B (2006) Lower bounds for energy of quadrangle-free graphs. MATCH Commun. Math. Comput. Chem, 55, 91-94.
- Chen A, Chang WC, Shiu (2006), Energy ordering of unicyclic graphs, MATCH Commun. Math. Comput. Chem., 55: 95–102.
- Cvetković DM, Doob M, Sachs H (1980) Spectra of graphs: theory and application (Vol. 87). Academic Pr.
- Gutman I, Zhou B (2006) Laplacian energy of a graph. Linear Algebra and its applications, 414: 29-37.
- Liu J, Liu BA (2008) Laplacian-energy-like invariant of a graph, MATCH Commun. Math. Comput. Chem, 59: 355-372.
- Liu B, Huang ZY (2011) A survey on the Laplacian-energy-like invariant, MATCH Com- mun. Math. Comput. Chem, 66: 713-730
- Stevanovi´c D, lli´c A, Onisor C, Diudea MV (2009) LEL−a newly designed molecular descrip- tor, Acta Chim. Sloven, 56: 410-417.
- Gutman I, Zhou B, Furtula B (2010) The Laplacian-energy like invariant is an energy like invariant, MATCH Commun. Math. Comput. Chem, 64: 85-96
- Gutman I, Markovi´c S, Vesovi´c A, Estrada E (1998) Approximating total π-electron energy in terms of spectral moments. A quantitative approach, J. Serb. Chem. Soc., 63: 639–646.
- Stevanovi´c D (2009) Laplacian-like energy of trees, MATCH Commun. Math. Comput. Chem, 61: 407-417.
- Read RC, Wilson RJ (1998) An Atlas of Graphs, The Clarendon Press Oxford University Press, NewYork.

Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences