ISSN : 2349-3917
American Journal of Computer Science and Information Technology
Detecting tÃÆââ¬Å¾ÃâÃÂla Computationally in Polyphonic Context-A Novel Approach
Susmita Bhaduri*, Anirban Bhaduri and Dipak Ghosh
Deepa Ghosh Research Foundation, Maharaja Tagore Road, India
- *Corresponding Author:
- Susmita Bhaduri
Deepa Ghosh Research Foundation, Maharaja Tagore Road, India
Tel: 919836132200
E-mail: susmita.sbhaduri@gmail.com
Received date: October 01, 2018; Accepted date: October 04, 2018; Published date: October 29, 2018
Citation: Bhaduri S, Bhaduri A, Ghosh D (2018) Detecting tāla Computationally in Polyphonic Context-A Novel Approach. Am J Compt Sci Inform Technol Vol.6 No.3:30 DOI: 10.21767/2349-3917.100030
Copyright: © 2018 Bhaduri S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In North-Indian-Music-System (NIMS), tablā is mostly used as percussive accompaniment for vocal-music in polyphonic-compositions. The human auditory system uses perceptual grouping of musical-elements and easily filters the tablā component, thereby decoding prominent rhythmic features like tāla, tempo from a polyphoniccomposition. For Western music, lots of work has been reported for automated drum analysis of polyphoniccomposition. However, attempts at computational analysis of tāla by separating the tablā-signal from mixed signal in NIMS have not been successful. Tablā is played with two components-right and left. The right-hand component has frequency overlap with voice and other instruments. So, tāla analysis of polyphonic-composition, by accurately separating the tablā-signal from the mixture is a baffling task, therefore an area of challenge. In this work we propose a novel technique for successfully detecting tāla using left-tablā signal, producing meaningful results because the left-tablā normally doesn't have frequency overlap with voice and other instruments. North-Indianrhythm follows complex cyclic pattern, against linear appro ach of Western-rhythm. We have exploited this cyclic property along with stressed and non-stressed methods of playing tablā-strokes to extract a characteristic pattern from the left-tablā strokes, which, after matching with the grammar of tāla-system, determines the tāla and tempo of the composition. A large number of polyphonic (vocal+tablā +other-instruments) compositions have been analyzed with the methodology and the result clearly reveals the effectiveness of proposed techniques.
Keywords
Left-tablā drum; Tāla detection; Tempo detection; Polyphonic composition; Cyclic pattern; North Indian Music System-NIMS
Introduction
Current research in Music-information-Retrieval (MIR) is largely limited to Western music cultures and it does not address the North-Indian-Music-System hereafter NIMS, cultures in general. NIMS raise a big challenge to current rhythm analysis techniques, with a significantly sophisticated rhythmic framework. We should consider a knowledge-based approach to create the computational model for NIMS rhythm. Tools developed for rhythm analysis can be useful in a lot of applications such as intelligent music archival, enhanced navigation through music collections, content based music retrieval, for an enriched and informed appreciation of the subtleties of music and for pedagogy. Most of these applications deal with music compositions of polyphonic kind in the context of blending of various signals arising from different sources. Apart from the singing voice, different instruments are also included.
As per rhythm relates to the patterns of duration that are phenomenally present in the music [1]. It should be noted that that these patterns of duration are not based on the actual duration of each musical event but on the Inter Onset Interval (IOI) between the attack points of successive events. As per Grosvenor et al., an accent or a stimulus is marked for consciousness in some way [2]. Accents may be phenomenal, i.e. changes in intensity or changes in register, timbre, duration, or simultaneous note density or structural like arrival or departure of a cadence which causes a note to be perceived as accented. It may be metrical accent which is perceived as accented due to its metrical position [3]. Percussion instruments are normally used to create accents in the rhythmic composition. The percussion family which normally includes timpani, snare drum, bass drum, cymbals, triangle, is believed to include the oldest musical instruments, following the human voice [4]. The rhythm information in music is mainly and popularly provided by the percussion instruments. One simple way of analyzing rhythm of a composite or polyphonic music signal having some percussive component, may be to extract the percussive component from it using some source separation techniques based on frequency based filtering. Various attempts have been made in Western music to develop applications for re-synthesizing the drum track of a composite music signal, identification of type of drums played in the composite signal (ex. the works of Gillet et al. and Nobutakaet al. etc., described in the below section in detail) [5,6]. Human listeners are able to perceive individual sound events in complex compositions, even while listening to a polyphonic music recording, which might include unknown timbres or musical instruments. However designing an automated system for rhythm detection from a polyphonic music composition is very difficult.
In this work we propose an absolutely novel approach of detecting tāla from classical and semi classical North Indian polyphonic music compositions. The rest of the paper is organized as follows. Some relevant definitions of North-Indian- Music-System (NIMS) are provided in definitions. A review of past work is presented in the novelty of proposed method and further research details are elaborated in the respective section.
Definitions
Tāla and its structure in NIMS
The basic identifying features of rhythm or tāla in NIMS are described as follows.
• Tāla and its cyclicity: North Indian music is metrically organized and it is called nibaddh (bound by rhythm) music. This kind of music is set to a metric framework called tāla. Each tāla is uniquely represented as cyclically recurring patterns of fixed time-lengths.
• āvart: This recurring cycle of time-lengths in a tāla is called āvart. vart is used to specify the number of cycles played in a composition, while annotating the composition.
• Mātra: The overall time-span of each cycle or āvart is made up of a certain number of smaller time units called mātra-s. The number of mātra-s for the NIMS tāla-s, usually varies from 6 to 16.
• Vibhāga: The mātra-s of a tāla are grouped into sections, sometimes with unequal time-spans, called vibhāga-s.
• Bol: In the tāla system of North Indian music, the actual articulation of tāla is done by certain syllables which are the mnemonic names of different strokes/pulses corresponding to each mātra. These syllables are called bol-s. There are four types of bol-s as defined below.
• Sam: The first mātra of an āvart is referred as sam which is mandatorily stressed [7].
• Tāli-bol: Tāli-bol-s are usually stressed, whereas khāli-s are not. Tāli -bol-s are gestured by the tablā player with claps of the hands, hence are called sasabda kriya. The sam is almost always a Tali-bol for most of the tāla-s, with only exception of rupak tāla which designates the sam with a moderately stressed bol called khali (as explained below) [8]. Highly stressed vibhāga boundaries are indicated through the tālibols [8]. Tāli-sam is indicated with a (+) in the rhythm notation of NIMS. Consequent Tāli-vibhāga-boundaries are indicated with 2,3…
• Khali-bol: Khali literally means empty and for NIMS it implies wave of the hand or nisabda kriya. Moderately stressed Vibhāga boundaries are indicated through the khali-bols so we almost never find the khali applied to strongly stressed bol-s like sam [8]. Khali-sam is indicated with a (0) in the rhythm notation of NIMS and consequent khali-vibhāgaboundaries are indicated also with 0.
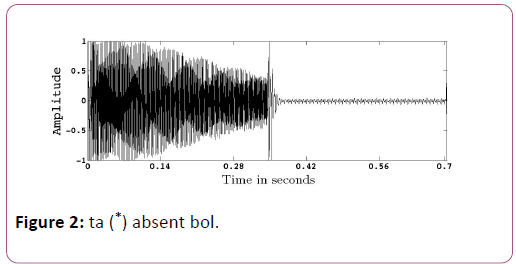
• Absent-bol: Sometimes while playing tablā, certain bol-s are dropped maintaining the perception of rhythm intact. They are called rests and they have equal duration as a bol. We have termed them as absent strokes/bol-s. These bol-s are denoted by (*) in the rhythm notation of a NIMS composition Ancient-future. In the Figure 2, the waveform of absent bol, denoted by (*), is shown just after another bol ta, played in a tablā-solo. Normally in a NIMS composition there may be many absent bol-s in the thekā played for the tāla. In these cases other percussive instruments(other than tablā) and vocal emphasis might generate percussive peaks for the time positions of the absent strokes, depending on the composition, the lyrics being sung and thus the rhythm of the composition is maintained.
• Thekā: For tablā, the basic characteristic pattern of bol-s that repeats itself cyclically along the progression of the rendering of tāla in a composition is called thekā. In other words it’s the most basic cyclic form of the tablā [8]. Naturally thekā corresponds to the basic pattern of bol-s in an āvart. The strong starting bol or sam along with the tālivibhāga- boundaries in a thekā carries the main accent and creates the sensation of cadence and cyclicity.
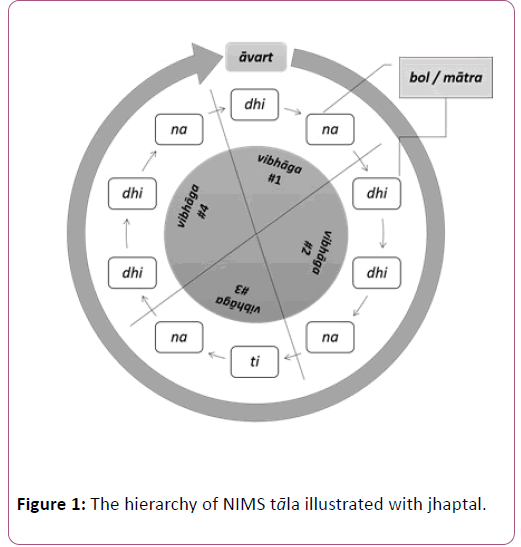
Description of the definitions with an example: The details of these theories are shown in the structure of a t la, called jhaptal in the Table 1 and Figure 1. The hierarchy of the features and their interdependence are shown in the Figure 1. The cyclic property of tāla is evident here.
| tā li | + | 2 | 0 | 3 | ||||||
| bol | Dhi | na | dhi | dhi | Na | ti | na | dhi | dhi | na |
| mātrā | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| vibhāga | 1 | 2 | 3 | 4 | ||||||
| āvart | 1 |
Table 1: Description of jhaptal, showing the structure and the its basic bol-pattern or the thekā
• The first row of Table 1 shows the sequence of tali-s and the khali-s in a thekā or āvart of jhaptal. In this row the sam is indicated with a (+) sign and it should be noted that for jhaptal it is a tali-bol. The second tāli-vibhāga-boundary is denoted by (2) followed by a (0) as it is the first khalivibhaga- boundary and then by one more tali denoted by (3) in a single cycle or thekā.
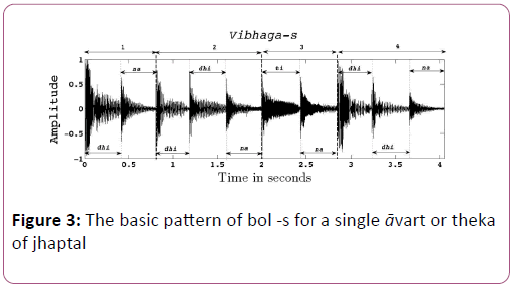
• The amplitude waveform of the same thekā is shown in the Figure 3. The sam is shown in the Figure as the first bol dhi. This clip of jhaptal is available in Tabla Radio.
• The second row of the Table 1 shows the bol-s of jhaptal in its thekā. In the Figure 3 the waveform of all these bol-s of a single cycle of jhaptal are shown.
• Jhaptal thekā comprises of ten mātrā -s which are shown as per their sequence in third row of Table 1.
• In the fourth row of the Table 1, the section or vibhāgaboundary- positions and sequences are shown. These vibhāga-sequences are shown for jhaptal in the Figure 3. We can see that there are four vibhāga-s in jhaptal theka and first vibhāga-boundary is a tāli-sam-bol dhi having mātrā number as one. Second vibhāga-boundary is again tāli-bol dhi having mātrā number as three and so on.
In the fourth row of the Table 1, āvart-position and sequence is shown. As there is one cycle shown so āvart-sequence is 1.
Tablā and bol-s
Tablā, the traditional percussive accompaniment of NIMS, consists of a pair of drums. Bayan the left drum, is played by the left hand and made with metal or clay. It produces loud resonant or damped non-resonant sound. As bayan cannot be tuned significantly, when it is played, it produces a fixed range of frequencies. The dayan is the wooden treble drum, played by the right hand. A larger variety of acoustics is produced on this drum when tuned in different frequency ranges. In the tāla system of North Indian music, the representation of tāla is done mainly by playing bol-s on the tablā. bol-s as they are played in tablā are listed in Table 2. Figures 4-6 show the waveform of few sample waveforms of the bol-s te, dha and ge respectively. The clip of the bol-s are taken from Tabla Radio.
| played on bayan | played on dayan | played on both bayan and dayan |
| ke, ge, ghe, kath | na, tin, tun, ti, te, ta, da | dha (na+ge), dhin (tin+ge), dhun (tun+ge), dhi (ti+ge) |
Table 2: List of commonly played bol-s in either on bayan or dayan or together on both.
Most of the tāla-s have tāli-sam played either with bayan alone or with bayan and dayan played simultaneously [8]. Same thing happens for the tāli-vibhāga boundaries. Most of the North Indian classical, semi-classical, devotional and popular songs are played as per the tāla-s in Table 3. The most commonly played thekā-s are shown in this Table, Ref. Tabla Class; TAALMALA-THE RHYTHM OF MUSIC. For our experiment, we have considered the thekā-s listed in the Table 6 for the tālas dadra, kaharba, rupak and bhajani. For these thekā-s, the stressed bol-s having a bayan component is shown in bold and pipes in bold indicate vibhāga boundary.
| tāla | Number of mātrā-/vibhā ga in an āvart | thekā |
|---|---|---|
| dadra | 3 I 3 | dha dhi na | na ti na |
| kaharba | 4 I 4 | dha ge na ti | na ke dhi na |
| rupak | 3 I 2 I 2 | tun na tun na ti te | dhin dhin dha dha | dhin dhin dha dha |
| bhajani | 4 I 4 | dhin*na dhin*dhin na*| tin*na tin*tin na* |
| jhaptal | 2 I 3 I 2 I 3 | dhi na | dhi dhi na | ti na | dhi dhi na |
| tintal | 4 I 4 I 4 I 4 | dha dhin dhin dha | dha dhin dhin dha | na tin tin na | te-Te dhin dhin dha |
Table 3: Table of popular thekā-s of North Indian rhythms.
It is evident from the Table 3 that all the tāla-s except rupak, start with a tali-sam-bol having both dayan and bayan component. Only rupak starts with a khali-sam and its sam does not contain any bayan component. Bhajani tāla, is often played with a variation for bhajan, kirtan or qawwali songs [9], which makes the first (tali-sam) and fourth bol as stressed. Although this fourth bol is not a tali vibhaga boundary still it is rendered as stressed and it is to be noted here that this bol is played with dayan and bayan together. We have considered this bhajani theka with first (tali-sam) and fourth bol as stressed, because data in our experiment includes popular bhajan or devotional compositions.
For the tāla-s dadra and kaharba the number of pulses in the theka and the matra-s are identical but for rupak and bhajani each matra is divided in to two equal duration bol-s. In effect rupak is a 7 mātrā tāla but has 14 pulses or bol-s and bhajani is 8 mātrā tāla but has 16 pulses or bol-s. Bhajani thekā in the Table 3 has half of its number of strokes as absent bol-s or rests (denoted by*).
It should be noted that the standard thekā of rupak is tin|tin| tin|na|dhin|na|dhin|na, but we have taken another thekā shown in the Table 3 for our experiment. This thekā is normally followed for the semi-classical soundtracks and popular hindi songs. Moreover, we got maximum number of annotated samples of polyphonic songs composed with this thekā for our validation process.
Lay or tempo
An important concept of rhythm in NIMS is lay, which governs the tempo or the rate of succession of tāla. The lay or tempo in NIMS can vary among ati-vilambit (very slow), vilambit (slow), madhya (medium), dr̥uta (fast) to ati-dr̥uta (very fast). Tempo is expressed in beats per minute or BPM.
Based on the definitions of the current section a detailed survey of the previous works in the rhythm analysis area both in Western and Indian music is elaborated in the following section.
Past work
Although various rhythm analysis activities have been done for Western music, not much significant work has been done in the context of NIMS. Although the rhythmic aspect of Western music is much simpler in comparison to Indian one, to get the broad idea of the problem, our study includes the work on Western music. The extraction of percussive events from a polyphonic composition is an ongoing and challenging area of research. We have discussed existing drum separation approaches in Western music in 4, as they are relevant to our methodology. The existing works in meter analysis and beattracking for Western music, are discussed in the following section. Then similar discussion is made on existing rhythm analysis works in Indian music.
Meter analysis in Western music
In Western music beats have sharp attacks, fast decays and are uniformly repeated while in Middle Eastern and Indian music beats have irregular shapes. This is due the fact that bass instruments in these cultures are different from what is used in Western bands. By examining the distribution of Western meters, Alghoniemy and Tewfik found that they deviate from Gaussianity by a larger amount than non-western meters [10].
Works have been done by parsing MIDI data into rhythmic levels by Rosenthal et al. [11]. But that cannot deal real audio data, attempted to encode the musical texts, notes into sequence of numbers and ± signs [12]. But it can be implemented only for the Western compositions for which the notation is available.
Todd and Brown [13] showed multi-scale mechanism for the visualization of rhythm as rhythmogram. The rhythmogram provides a representation to the structure of spoken words and poems used, which is very different from polyphonic music but the model is implemented on synthesized binary pattern, strong and weak pulses, not from actual music composition.
Alghoniemy and Tewfik [10] analysed the beat and rhythm information with a binary tree or trellis tree parsing depending on the length of the pauses in the input polyphonic signal. The approach relies on beat and rhythm information extracted from the raw data after low-pass filtering. It has been tested using music segments from various cultures.
Foote et al. [14], described methods for automatically locating points of significant change in music or audio, by analysing local self-similarity. This approach uses the signal to model itself, and thus does not rely on particular acoustic cues nor requires training.
Klapuri and Astola [15] describes a method of estimating the musical meter jointly at three metrical levels of measure, beat and subdivision, which are referred to as measure, tactus and tatum, respectively. For the initial time-frequency analysis, a new technique is proposed which measures the degree of musical accent as a function of time at four different frequency ranges. This is followed by a bank of comb filter resonators which extracts features for estimating the periods and phases of the three pulses. The features are processed by a probabilistic model which represents primitive musical knowledge and uses the low-level observations to perform joint estimation of the tatum, tactus, and measure pulses.
Gouyon and Herrera [16] addressed the problem of classifying polyphonic musical audio signals of Western music, by their meter, whether duple/triple. Their approach aimed to test the hypothesis that acoustic evidences for downbeats can be measured on signal low-level features by focusing especially on their temporal recurrences.
Beat-tracking in Western music
In the work of Bhat [17], a beat tracking system is described. A global tempo is first estimated. A transition cost function is constructed based on the global tempo. Then dynamic programming is used to find the best-scoring set of beat times that reflect the tempo.
In Goto and Muraoka [18] a real-time beat tracking system is designed, that processes audio signals that contain sounds of various instruments. The main feature of this work is to make context-dependent decisions by leveraging musical knowledge represented as drum patterns
In Scheirer [19], the envelope of the music signal is extracted at different frequency bands. The envelope information is then used to extract and track the strokes/pulses.
To classify percussive events embedded in continuous audio streams, [20] relied on a method based on automatic adaptation of the analysis frame size to the smallest metrical pulse, called the tick.
Dixon [21] has created a system named Beat Root for automatic tracking and annotation of strokes for a wide range of musical styles. Davies and Plumbley [22] proposed a context dependent beat tracking method which handles varying tempos by providing a two state model. The first state tracks the tempo changes, then the second maintains contextual continuity within a single tempo hypothesis. Böck et al. [23]proposed a data driven approach for beat tracking using context-aware neural networks.
Rhythm analysis in Indian Music
The concepts of tāla and its elements are briefed in above section. For Indian percussive systems, strokes are of irregular nature and mostly are not of same strength. In comparison with Western music, not much significant work in rhythm analysis in Indian music has been reported so far.
Rhythm analysis and modeling for Indian music can be traced back to the study of acoustics of Indian drums by Sir C. V. Raman. In this work, the importance of the first three to five harmonics which are derived from the drum-head’s vibration mode was highlighted. In the last decade, most of the MIR research on Indian music rhythm has been focused on drum stroke transcription, creative modeling for automatic improvisation of tablā and predictive modeling of tablā sequences. Bhat [17] extended Raman's work and to explain the presence of harmonic overtones, he applied a mathematical model of the vibration modes of the membrane of a type of Indian musical drum called mridanga. Goto and Muraoka [18] were first to achieve a reasonable accuracy for tempo analysis on audio signals operated in real time. Their system was based on agent based architecture and tracking competing meter hypotheses. Malu and Siddharthan [25] confirmed C.V. Raman’s conclusions on the harmonic properties of Indian drums, and the tablā in particular. They accredited the presence of harmonic overtones to the central black patch of the dayan. Patel et al. [26] performed an acoustic and perceptual comparison of tablā bol-s (both, spoken and played). They found that spoken bol-s have significant correlations with played bol-s, with respect to acoustic features like spectral flux, centroid etc. It also enables untrained listeners to match the drum sound with corresponding syllables. This gave strong support to the symbolic value of tablā bol-s in North Indian drumming tradition.
Gillet et al. [5] worked on tablā stroke identification. Their approach had three steps: stroke segmentation, computation of relative durations (using beat detection techniques), and stroke recognition, after which they used the Hidden Markov Model (HMM) for transcription. But their work is mostly intended for rhythm transcription. Gouyon and Herrera [16] suggested a method to detect rhythm type, where the beat indices are manually extracted and then an autocorrelation function is computed on selected low level features like-spectral flatness, energy flux, energy in upper half of the first bark band. This helped in the advancing the beat-tracking algorithms.
State of the Art Works: The system proposed by Rae uses Probabilistic Latent Component Analysis method to extract tablā signals from polyphonic tablā solo [27]. Then each separated signal is re-synthesized in each layer and the music is regenerated in quida (improvisation of tablā performances) model. The work is restricted to tablā solo performances where the tablā signal is the most significant component, and not for polyphonic compositions where tablā is one of the percussive accompaniment.
In Gulati and Rao the work of Schuller et al. is extended [28,29]. The methodology for meter detection in Western music is applied for Indian music. A two-stage comb filter-based approach, originally proposed for double/triple meter estimation, is extended to a septuple meter (such as 7/8 timesignature). But this model does not conform to the tāla system of Indian music.
Miron [30] explored various techniques for rhythm analysis based on the Indian percussive instruments. An effort is made to extract the tablā component from a polyphonic music by estimating the onset candidates with respect to the annotated onsets. Various existing segmentation techniques for annotating polyphonic tablā compositions, were also tried. But the goal of automatic detection of tāla in Indian music did not succeed.
Some work has been done to detect a few important parameters like mātrā, tempo by first using signal level properties and then using cyclic properties of tāla. The work in Bhaduri et al. [31] for mātrā and tempo detection for NIMS tālas, is based on the extraction of beat patterns that get repeated in the signal. Such pattern is identified by processing the amplitude envelope of a music signal. Mātrā and tempo are detected from the extracted beat pattern. This work is extended to handle different renderings of thekā-s comprised of single and composite bol-s. In this work Bhaduri et al. [32] bol duration histogram is plotted from the beat signal and the highest occurring bol-duration is taken as the actual bol-duration of the input beat signal. The above methodology has been tested on electronic tablā signal. In case of the real tablā signal it is impossible to maintain consistency in terms of the periodicity of the bol-s or beat-s played by a human. To resolve this issue the work is further extended and modified to handle real tablā signal and this comparison is carried out for the entire beat signal and a weight-age or the probability of the experimental signal being played according to certain tāla-s of NIMS, is calculated [33]. The mātrā of the tāla for which this weightage is maximum, is confirmed as the mātrā of the input signal. This methodology was tested with real-tablā-solo performance recordings. In recent times experiments and analysis have been done with non-stationary, nonlinear aspects of NIMS [34].
It is evident from the study that rhythm analysis in NIMS, focusing on tāla rendered with tablā, the most popular North Indian percussive instrument, is a wide area of research. In our work, an approach for rhythm analysis is proposed, which is built around the theory of tāla in NIMS. On the background of the past works in the related field, the novelty of our approach is elaborated in the following section.
The Novelty of the Proposed Method
In the context of NIMS rhythm popularly known as tāla, tablā is the most popular percussive instrument. Its right hand drumdayan and left hand drum-bayan are played together and amplitude-peaks spaced at regular time intervals, are created by playing every stroke. One way of rhythm information retrieval from polyphonic composition having tablā as one of the percussive instruments, may be to extract the tablā signal from it and analyze it separately. The dayan has a frequency overlap with other instruments and mostly human-voice for polyphonic music, so if we extract the whole range of frequencies for both bayan and dayan components, by existing frequency based filtering methods, the resultant signal will be a noisy version of original song as it will still have part of other instruments, human voice components along with tablā. Also conventional source separation methods lead to substantial loss of information or sometimes addition of unwanted noise. This is the area of challenge in tāla analysis for NIMS. Although, NIMS tāla functions in many ways like Western meter, as a periodic, hierarchic framework for rhythmic design, it is composed of a sequence of unequal time intervals and has longer time cycles. Moreover tāla in NIMS is distinctively cyclical and much more complex compared to Western meter [35]. This complexity is another challenge for tāla analysis.
Due to the above reasons defining a computational framework for automatic rhythm information retrieval for North Indian polyphonic compositions is a challenging task. Very less work has been done for rhythmic information retrieval from a polyphonic composition in NIMS context. In Western music, quite a few approaches are followed for this purpose, mostly in the areas of beat-tracking, tempo analysis, annotation of strokes/pulses from the separated percussive signal. We have described these systems above. For NIMS, very few works of rhythm analysis are done by adopting Western drum-event retrieval system. These works result in finding out meter or speed which is not very significant in the context of NIMS. Hence this is an unexplored area of research for NIMS.+
In this work we have proposed a completely new approach, i.e.instead of extracting both bayan and dayan signal, we have extracted only the bayan signal from the polyphonic composition by using band-pass filter. This filter extracts lower frequency part which normally does not overlap with the frequency of human voice and other instruments in a polyphonic composition. Most of the tāla-s start with a bol or stroke which has a bayan component(either played with bayan alone or both bayan and dayan together) and also the some consequent section(vibhāga in NIMS terminology) boundary-bols have similar bayan component. Hence these strokes would be captured in the extracted bayan signal. For a polyphonic composition, its tāla is rendered with cyclically recurring patterns of fixed time-lengths. This is the cyclic property of NIMS, discussed in detail in the above section. So after extracting the starting bol-s and the section boundary strokes from the bayan signal, we can exploit the cyclic property of a tāla and the pattern of strokes appearing in a single cycle and can detect important rhythm information from a polyphonic composition. This would be a positive step towards rhythm information retrieval from huge collection of music recordings for both film music and live performances of various genres of hindi music. Here, we consider the tāla detection of different single-channel, polyphonic clips of Hindi vocal songs of devotional, semi-classical and movie soundtracks from NIMS, having variety of tempo and mātrā-s.
Proposed Methodology
As it has been already discussed that there is a frequency overlap between tablā (bayan and dayan ) with voice and other instruments in a polyphonic composition, accurate extraction of tablā signal from the mixed signal by following the source separation techniques based on frequency based filtering has not been very successful [36,37]. Also these source separation methods lead to substantial loss of information or sometimes addition of unwanted noise. It has motivated us to look for an alternate approach. Here we have adopted a four-step methodology which is detailed out in following sections.
• First we have processed the polyphonic input signal by partially adopting a filter-based separation technique. In doing so we are able to separate out the bayan-stroke-signal which would consist of the only bayan-strokes and also the bayan-components of bayan+dayan-strokes.
• Then further, we have processed the entire polyphonic signal and generated a peak-signal, which comprises of all the emphasized peak-s generated out of tablā and other percussive instruments played in the polyphonic composition of a specific tāla. Peak-signal would contain the peak-s of bayan-stroke-signal, and also the emphasized peak-s of tablā (i.e. only dayan -strokes and bayan+dayan-strokes). If other percussive instruments played, then in addition to the above, the peak-signal would also contain emphasized peak-s generated out of them
• Next we have refined the bayan-stroke-signal and the peaksignal.
• Lastly we propose to generate a co-occurrence matrix from both kinds of signals and exploit domain specific information of tablā and tāla theory, to detect the tāla and tempo of the input polyphonic signal.
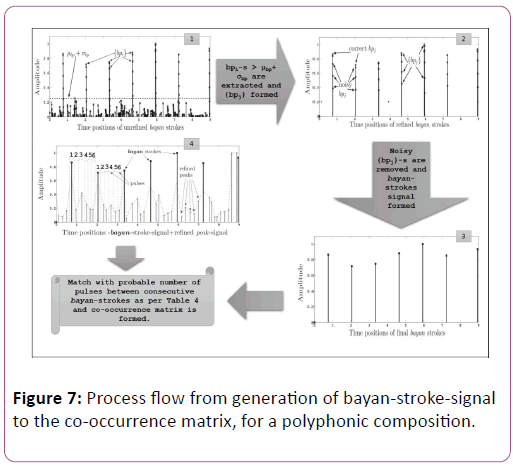
Overall flow of the process starting from generation of bayanstroke- signal to the final co-occurrence matrix is shown in the Figure 7, for a test clip composed in dadra tāla. The process of generating final bayan-stroke-signal [sub-figure 3] and final peak-signal (sub-figure 4) are described.
Separation of bayan-stroke-signal
In Western music drum is one of the mostly used percussive instruments. Extraction of drum signal is a part of applications like identification of type of drums, re-synthesizing the drum track of a composite music signal. Existing approaches for drum signal separation and our method of extracting bayan-strokesignal is described at various sections.
Drum separation approaches in Western music
• Blind Source Separation method: Christian Uhle, Christian Dittmar, Thomas Sporer [36] proposed a method based on Independent Subspace Analysis method to separate drum tracks from popular Western music data. In the work of Helén and Virtanen [37], a method has been proposed for the separation of pitched musical instruments and drums from polyphonic music. Non-negative Matrix Factorization (NMF) is used to analyze the spectrogram and thereby to separate the components.
• Match and adapt method: The methodology defines the template (temporal as stated in [38] or spectral as stated in [39], of drum sound, then searches for similar patterns in the signal. The template is updated and also improved in accordance with those observations of patterns. This set of methods extracts as well as transcripts drum component.
• Discriminative model: This approach is built upon a discriminative model between harmonic and drums sounds. In the work of Gillet and Richard [40], music signal is split into several frequency bands, the for each band the signal is decomposed into deterministic and stochastic part. The stochastic part is used to detect drum events and to resynthesize a drum track. Possible applications include drum transcription, remixing, and independent processing of the rhythmic and melodic components of music signals. Ono et al [6] have proposed a method that exploits the differences in the spectrograms of harmonic and percussive components.
Our approach: Our approach for separating out bayan-strokesignal falls in the Discriminative model group for separating out harmonic and drums sounds, among the three categories described above.
To extract the bayan-stroke-signal we have used ERB or Equivalent Rectangular Bandwidth filter banks. The ERB is a measure used in psychoacoustics, which gives an approximation to the bandwidths of the filters in human auditory system [41]. Alghoniemy and Rosenthal [10] have done empirical study of western drums and confirmed that that they could extract the bass drum sequences by filtering the music signal with a narrow bandpass filter. Ranade [42] confirmed the same range (60-200 Hz) for the bass drum or bayan of Indian tablā. If we take ERB filter banks to extract different components like voice, tablā and other accompaniments from the polyphonic signal with sampling rate of 44100 Hz, the central frequency of the second bank comes out to be around 130 Hz and the bandwidth of around 60-200 Hz. It has been observed from the spectral and wavelet analysis of the different type of bayan-bol-s and Table 2 that their frequency ranges around the same central frequency and bandwidth. So we have divided the input polyphonic signal sampled at 44100Hz, into 20 ERB filter banks and extracted the second bank for constructing the bayan-stroke-signal. We have used MIRtoolbox to extract this frequency range from ERB filter banks.
As described earlier, most of the tāla -s in NIMS start with a highly stressed tāla-sam-bol played with bayan or bayan and dayan combined. Moreover tāla vibhāga boundaries are also usually stressed. Thus extracted bayan-stroke-signal would mostly consist of peak-s generated from tāla-sam-s and tālavibhāga boundaries. There might be presence of other highstrength- peak-s generated out of bol-s having bayan component, other than tāla-sam and tāla-vibhāga boundaries, for compositions with slow (20BPM) or very slow (10BPM) tempo. But for popular, semi-classical and filmy North Indian compositions, the tempo is moderate to fast. These compositions mostly do not have the emphasized, high strength bayan-peak-s other than tāla-sam, tāla-vibhāga boundaries in the bayan-stroke-signal. Even if these additional bol-s having bayan-component, produce peak-s in the bayan-stroke-signal, their strength is much weaker, compared to tāla-sam or tālavibhāga boundaries.
The process below is followed to remove these additional bols having bayan component, from the bayan-stroke-signal.
• Let {bpi} be the set of peak-s in the bayan-strokes-signal extracted from a polyphonic song-signal. Please note the Figure Figure 7(1), where {bpi}-s for a particular polyphonic sample of dadra tāla are shown.
• We calculate the mean -μbp and standard deviation -σbp for the set {bpi}. In the Figure 7 (1), the corresponding value of μbp+σbp is shown. It should be noted there are lots of noisy peak-s with magnitude less than μbp+σbp.
• {bpj} is obtained as a subset of {bpi} after selecting the highstrength bayan-strokes greater than μbp+σbp.
• {bpj} is the set of strokes mostly containing tāli-sam-s and tāli-vibhāga boundaries having bayan-component, for a polyphonic composition. In the Figure 7(2), the corresponding time positions of are shown.
• However, there would always be some noisy peak-s in {bpj}, hence a further refinement is done as per the described method and finally the refined bayan-stroke-signal is shown in the Figure 7(3).
Peak-signal
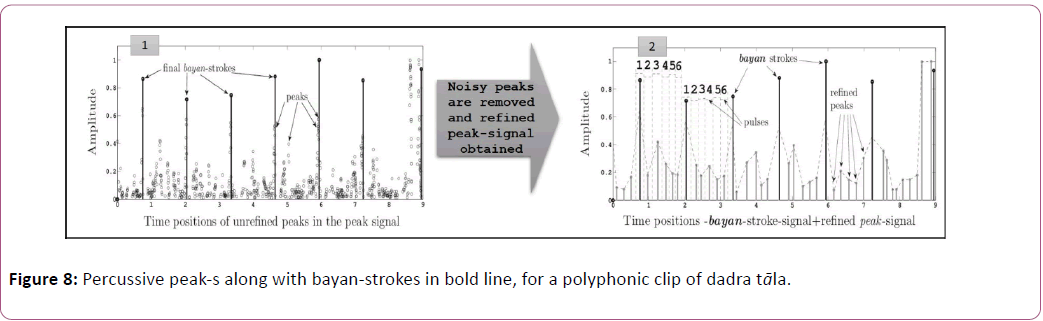
From the input polyphonic signal waveform, differential envelope is generated after applying half-wave rectifier. The peak-s is extracted from the amplitude envelope of the signal, by calculating the local maxima-s. Local maxima-s are defined as the peak-s in the envelope with amplitude higher than their adjoining local minima-s by a default threshold quantity of df × Imax, where Imax, is the maximum amplitude point of the envelope. Here we have taken default minimum value for df in the MIR toolbox [43], which would extract almost all the peak-s in the input envelope. Each peak in the peak-signal is mainly generated out of tablā and other percussive instruments played in the polyphonic composition. These peak-s are supposed to be more stressed than other melodic instruments and vocals rendered with comparatively more steady range of energies (without much ups and down, hence unable to produce highenergy peak-s). Figure 8 (1) shows all the peak-s along with the positions of the bayan-strokes of the bayan-stroke-signal in bold, for the same test clip of the Figure 7. The bayan-stroke-signal has been generated as per process in section our approach.
Refinement of bayan and peak-signal
There may be multiple percussive instruments and also human voice in a polyphonic composition. There is a tendency to stress more at the tāli-sam and tāli-vibhāga boundaries by the performer, while singing along with the tāla. Hence for polyphonic compositions, other percussive instruments and human voice also generate peak-s in the bayan-stroke-signal, coinciding with bayan-strokes.
Peak-signal for polyphonic signal also consists of peak-s produced by tablā, percussive instruments (if present) and human voice. For both bayan-stroke and peak signals, these peak-s should coincide with respect to their positions in X-axis or time of their occurrences. But among them the peak-s generated out of tablā or the drum instrument here, are usually of higher strength. Using this theory we go for refinement of both bayan-stroke-signal and peak-signal to retain the most of the peak-s generated from tablā, and discard other kinds of percussive peak-s. It has been observed that most of the popular Hindi compositions (classical or semi-classical) have tempo much less than 600 beats per minute [Rhythm Taal]. Thereby minimum beat interval or gap between consecutive tablā strokes in these compositions, is much more than 60/600=0.1sec.
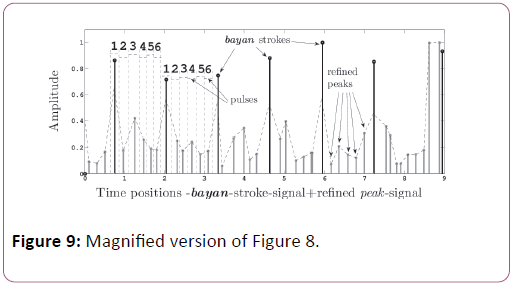
Hence both the bayan-stroke-signal and peak-signal are divided into 0.1 sec duration windows along X-axis. For each window the peak having highest strength is retained as correct bayan-stroke (in bayan-stroke-signal) or any other valid tablā peak (in peak-signal), and rest of the peak-s in each window is dropped. This way the noisy peak-s is removed and final bayanstroke- signal and peak-signal are obtained. Figure 8 (2) shows the final, high-strength and refined peak-signal, with the positions of the bayan-strokes of the refined bayan-stroke-signal in bold. The same final peak-signal is referred in Figure 7 (4). Figure 9 is the magnified version of Figure 8 (2) and Figure 7 (4).
Analysis based on tablā and tāla theory
The refined peak-signal for the same clip in dadra tāla is shown in Figure 9. As per the thekā of dadra in Table 3, apart from the sam-dha there is no other tāla-vibhāga boundaries, hence its final bayan-stroke-signal should contain these sam-s only.
• Pulse: Here pulse is defined as the amplitude envelope of a stroke whose peak is extracted in the peak-signal.
• Peak: It should be noted here that, a peak in the refined peak-signal, is the highest point of an amplitude envelope formed for a pulse. Hence peak is actually the mid-point of the pulse duration in seconds along the X -axis.
For the test clip of dadra tāla, the peak-s and the pulses are elaborated in Figure 9. Here we can see there are 5 peak-s and 6 pulses in between two consecutive bayan strokes.
The method of tāla detection based on tablā and tāla theory is explained in the following sections.
First level analysis of pulse pattern: As per the theories explained in section Tāla and its structure in NIMS and Tablā and bol-s, we have extended the Table 3 and created another Table 4. Here the first column describes number of probable pulses in between two bayan strokes, as per the theories. For example, for dadra tāla, number of pulses in between a dha-bol/sam of an āvart and the dha-bol/sam of the next āvart should theoretically be 6 as per the dadra thekā in the Table 4. This 6-6 pattern of number of pulses should continue along the progression of the composition. The third column describes the thekā-s corresponding to the pulse pattern, with tāla-sam-s and tālivibhāga- boundary-bol-s in bold as per the theory explained in section Tāla and its structure in NIMS and Tablā and bol-s The pipes in bold represent the start of vibhāga-boundaries within single āvart. Āvart-sequences are shown and for each thekā, a āvart and the starting bol of next āvart are given, to indicate the progression of tāla-s.
| Number of probable pulses between consecutive bayan-strokes āla-s | Tāla-s | Corresponding thekā-s with āvart-sequences |
| 6-6 | dadra | |1dha dhi na|na ti na|2dha.. |
| 8-8 | kaharba | |1dha ge na ti|na ke dhi na|2dha.. |
| 4-10,10-4 | rupak | |1tun na tun na ti te|dhin dhin dha dha|dhin dhin dha dha|2tun na.. |
| 14-14 | rupak | |1tun na tun na ti te|dhin dhin dha dha|dhin dhin dha dha |2 tun na.. |
| 3-13,13-3 | bhajani | |1dhin* na dhin*dhin na*|tin*ta tin*tin ta*|2dhin* .. |
| 16-16 | bhajani | |1dhin*na dhin*dhin na*|tin*ta tin*tin ta*|2dhin .. |
Table 4: Probable number of pulses in between consecutive bayan-strokes, corresponding thekā-s and the tāla-s.
It is to be noted that bhajani thekā has half of its number of strokes as rests. Other percussive instrument and vocal emphasis would normally generate peak-s of moderate strength for the time positions of these strokes in an āvart, especially for the genres of our experimental compositions. Hence, here bhajani is considered as tāla with16 pulses/āvart.
It should be noted that for tāla-s like bhajani and rupak, there are two sets of probable no of pulses. For example for rupak there is both 4-10 and10-4. This is because we are calculating number of pulses for the consecutive āvart along the progression of the song. So suppose if we start from āvart 1, the second vibhaga-boundary-bol has bayan component and it will generate a peak in the bayan-stroke-signal. Next peak in the bayan-stroke-signal would be the third vibhāga-boundary-bol. So in between them (I dhin dhin dha dha I dhin) there would be 3 peak-s and 4 pulses. Next peak in the bayan-stroke-signal would be the second vibhāga-boundary-bol of the āvart 2 and evidently there would be 9 peak-s and 10 pulses between second and third peak-s in bayan-stroke-signal (dhin dhin dha dha2 I tun na tun na ti te I dhin). It gives rise to pulse pattern of 4-10, considering first, second and third peak-s in bayan-strokesignal. Now if we move on and consider second, third and fourth bayan-peak-s, the detected pulse pattern should be10-4, then again 4-10 and it will go on for the entire progression of the song. So both 4-10 and10-4 would signify rupak tāla with same set of stressed bol-s in the thekā.
Extended analysis of pulse pattern: It should be noted that, in vilambit compositions there may be additional filler strokes apart from the basic thekā, which lead to additional significant peak-s in both the bayan-stroke-signal and the peak-signal. In druta compositions often several thekā strokes are skipped and only vibhāga-s are stressed.
Table 4 shows the elementary set of probable pulses in between consecutive bayan strokes for clear understanding of the concept. To keep room for variations and improvisations of the thekā that are allowed within a specific tāla, we have extended this set in our experiment. There we have included all the probable patterns of pulse-counts, by considering the probability of additional bayan or bayan+dayan -strokes in a thekā to be stressed. We are assuming that apart from the mandatory tāli-sam and tāli-vibhāga boundaries, any other bol-s having bayan component may be stressed and produce a peak in the bayan-stroke-signal.
Here we have shown all the probabilities (including basic and extended) for dadra tāla in Table 5, as an example. Here in this dadra-thekā apart from the tāli-sam-bol which is dha, of a āvart, the very next bol is dhi also has bayan-component. So apart from mandatory sam this bol can also be stressed and give rise to pulse pattern of 1-5, 5-1. Similarly for rest of the tāla-s, all probable combinations of number of pulses are calculated.
| Number of probable pulses between consecutive bayan-strokes | Corresponding thekā-s with āvart-sequences |
|---|---|
| 6-6 | |1dha dhi na|na ti na |2dha.. |
| 1-5, 5-1 | |1dha dhi na|na ti na |2dha dhi.. |
Table 5: Probable number of pulses in between consecutive bayan strokes in the thekā for dadra tāla.
Generation of co-occurrence matrix and detection of tāla: For each test sample, we have taken the refined version of bayan-stroke-signal, peak-signal (generated and refined as per the method in above section) and the co-occurrence matrix is formed and tāla is detected as per the following steps. Here cooccurrence matrix displays the distribution of co-occurring pulse-counts along the sequence of the bayan-stroke-intervals, in a matrix format The Figure 7 shows the overall process flow of generation of co-occurrence matrix from refined bayan-strokesignal and peak-signal.
• We extract the time positions of the peak-s of the refined peak-signal and the bayan-stroke-signal along the X-axis or time axis.
• Then we calculate the count of peak-signal-pulses occurring in each of the time intervals formed by consecutive peak-s of bayan-stroke-signal. Here we denote the series of pulsecounts calculated for a test-sample as (pc1, pc1… pck ) , where k=(number of bayan-strokes ). For example, we can see in the Figure 9, there are 5 peak-s between two consecutive bayanstrokes the number of pulses are 6 or pc1=6. Similarly, we calculate the rest of the pci-s.
• Then we form 16 ⨯ 16 co-occurrence matrix (having 16 rows and 16 columns/row) and initialize all of its elements with zero. Maximum dimension of the matrix is taken as 16 because for our test data there can be maximum of 16 numbers of pulses between consecutive bayan-strokes (Refer Table 4).
• Then we fill up the co-occurrence matrix by occurrence of each pair of pulse-counts between the consecutive intervals in the bayan-stroke-signal formed for the whole test sample. We denote each consecutive pair as pci+pc where pci ϵ (1, 2…16) and pc ϵ (1, 2…16). For example if the number of pulses between first and the second peak-s in the bayanstroke- signal is 4 and the same between the second and the third is 6. So pc1, pc2 becomes 4, 6 and we add 1 to the matrix element of fourth row and sixth column, which now becomes 1 from initialized zero value. Then we check the same between third and fourth peak which is suppose 6, hence pc2, pc3, becomes 6, 6 and now 1 is added to the matrix element of sixth row and sixth column, making it 1 from zero.
• We traverse the whole peak-signal and the bayan-strokesignal and update the matrix. Each cell of the matrix contain the occurrence of a particular pulse count pattern in consecutive intervals in bayan-stroke-signal.
• Finally we extract the row and column index of the cell in the matrix containing the maximum value. This row and column index is the most occurring pattern of pulse counts in consecutive intervals in bayan-stroke-signal. Here this rowcolumn index of the matrix is denoted by (pcmax1, pcmax2).
• The co-occurrence matrix for a test sample is shown in Table 6 where we can see 10 as the maximum value in 6th row and 6th column i.e. (pcmax1=pcmax6, pcmax2=6).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | … | |
| 1 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | … |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| 7 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | … |
| … | … | … | … | … | … | … | … | … |
Table 6: Co-occurrence matrix formed for a composition played in dadra-tāla
• Then the (pcmax1, pcmax2) is matched against the first column of the Table 4 and also the rules defined above. Accordingly ta ̅ la is decided from its second column. For the test sample for which the co-occurrence matrix is shown in the Table 6, pcmax1=6 and pcmax2=6 are extracted and it is exactly matched with 6-6 pattern for number of probable pulses between consecutive bayan-strokes, hence it is detected as of dadra tāla.
• While matching occurrence pattern of peak-s between consecutive bayan-peak-s, apart from the rules explained in section First level analysis of pulse pattern and extended analysis of pulse pattern, a tolerance of ± 1 considered. For example, if for a test clip we get 6-6 number of peak-s between consecutive bayan duration in the bayan-strokesignal, we detect it as of dadra tāla. But even if we get 6-5 or 5-6, then also detect it as dadra. This way we are considering human errors within a narrow range of tolerance.
Detection of tempo: Tempo or lay is detected in terms of pulses per minute as per the method below.
• Once we detect (pcmax1, pcmax2) we get the tāla as per the process described earlier. Then we collect all the consecutive pair of bayan durations having pcmax1 and pcmax2 number of pulses for the whole composition. In the Figure 9, we can see that for this particular dadra clip there are 6 number of pulses in the intervals between first two bayan-strokes and also second, third bayan-strokes.
• Suppose these bayan durations are denoted by (bd11, bd12… bd1n) having pcmax1 number of pulses and (bd21, bd22… bd2n) having pcmax2 number of pulses, where n is the value in the cell of co-occurrence matrix having row index pcmax1 and column index pcmax2. It basically means that (pcmax1, pcmax2) pair has occurred for n no of times in the cooccurrence matrix and also in the whole test composition.
• Then all these bayan durations are added. We denote that by  Total number
of pulses in these durations are countpulse=n*(pcmax1+
pcmax2). banyandur is measured in second.The average
duration of a pulse in the composition is calculated as
Total number
of pulses in these durations are countpulse=n*(pcmax1+
pcmax2). banyandur is measured in second.The average
duration of a pulse in the composition is calculated as  in second. Then the tempo is
calculated as
in second. Then the tempo is
calculated as ![]() in beats per minute.
in beats per minute.
Experimental Details
Data description
We have experimented with a number of polyphonic compositions of NIMS vocal songs rendered with four popular theka-s of the tāla-s, as described in Table 4. The test compositions are from bhajan or devotional, semi-classical and film-music genres, having tablā and other percussive instruments as accompaniments. The film-music and semiclassical genres are chosen because they mostly maintain similar structures with minimal improvisation and regular tempos as far as rhythm of the compositions are concerned. Hence this test dataset should be suitable for finalizing the elementary layer of the tāla-detection system of NIMS.
The tāla-s considered are dadra, kaharba, rupak, bhajani, as most of the songs in above genres are composed in these tāla-s. Also we got maximum number of annotated samples of polyphonic songs composed with these tāla-s, which helped in rigorous testing and validation process. Also as these tāla-s have unique mātra-s and they would produce mostly unique number of peak-s between consecutive bayan-strokes, so experimenting with sufficient number of test samples composed in these tāla-s enabled us to validate the applicability of the initial version of our model.
The annotated list of tāla-wise songs are obtained from Sound of India and FILM SONGS IN VARIOUS TALS and also from the albums The Best Of Anup Jalota (Universal Music India Pvt Ltd), Bhanjanjali vol 2 (Venus), Bhajans (Universal Music India Pvt Ltd), Songs Of The Seasons Vol (Shobha Gurtu). The annotations are validated by renowned musician Subhranil Sarkar. All the song clips are in single channel .wav format sampled at 44100Hz and are annotated. The clips are of 60 second duration. The tempo ranges from madhya to ati-druta tempo. The tempo of the input samples were calculated by manual tapping by expert musicians and this calculated tempo were assumed to be our benchmark for validation. The detailed description of the data used is shown in Table 7. The tempo is uniformly maintained for the input sound samples of the experiment. The data reflects variation in terms of genre, types of instruments and voices in the composition, tempo and mātrā of the compositions.
| ta ̅ la | ma ̅ tra ̅ | Tempo range (in BPM) | No of clips |
|---|---|---|---|
| dadra | 6 | 140-320 | 65 |
| kaharba | 8 | 220-400 | 65 |
| bhajani | 8 | 300-360 | 65 |
| rupak | 7 | 240-375 | 65 |
Table 7: Description of data.
Results
Table 8: Confusion matrix for tāla detection for the clips (all figures in %).
| dadra | kaharba | bhajani | rupak | none | |
|---|---|---|---|---|---|
| dadra | 80.85 | 6.38 | 6.38 | 4.26 | 2.13 |
| kaharba | 4.17 | 81.25 | 8.33 | 2.08 | 4.16 |
| bhajani | 3.57 | 12.5 | 78.57 | 3.57 | 1.79 |
| rupak | 3.5 | 4.5 | 4 | 86 | 2 |
Table 8: Confusion matrix for tāla detection for the clips (all figures in %).
Table 8 shows the confusion matrix for tāla detection. Here the column none signifies that the tāla of the input clip is NOT detected as any of the input tāla-s (dadra, kaharba, rupak, bhajani). There is an incorrect detection between the pair of kaharba and bhajani. Few bhajani samples have been detected as kaharba and vice-versa. For a specific laggi or variation of bhajani tāla Bhajan taal, a composition might turn out to be with 8-8 pulse pattern where [pcmax1=8, pcmax2=8]. In this case it would be detected as kaharba as per our method. However, this error is not so severe as technically bhajani is a variation of kaharba [8].
Also as per the Table 4 theoretically 8-8 pulse pattern is for kaharba and 16-16 is for bhajani, i.e. pattern for bhajani is exactly twice of kaharba. For some rare cases of manual error, while playing tablā in kaharba, the tablā-expert might make some sam-s less stressed and this sam-s might fail to generate bayan-peak-s in the refined bayan-stroke-signal. In these cases kaharba might produce16-16 pulse pattern and would be detected as bhajani. However, this is much rare as theoretically for any tablā composition the tāli-bol-sam must be stressed.
Table 9 shows the performance of proposed methodology in detecting tempo for different compositions. In judging the correctness of tempo, a tolerance of ± 5% is considered.
| Ta ̅ la | Correct detection |
|---|---|
| dadra | 80.85 |
| kaharba | 77.08 |
| bhajani | 80.35 |
| rupak | 76 |
Table 9: Performance of tempo detection (all figures in %).
Overall tāla and tempo detection performance is shown in Table 10 Gross performance of tāla and tempo detection (all figures in %). It is clear that the proposed methodology performs satisfactorily and that too with wide variety of data.
| Average performance | |
|---|---|
| ma ̅ tra ̅ detection | Tempo detection |
| 81.59 | 78.6 |
Table 10: Gross performance of tāla and tempo detection (all figures in %).
Conclusion
• This paper presents the results of analysis of tablā signal of North Indian polyphonic composition, with the help of new technique by extracting the bayan signal.
• The justification of using bayan signal as the guiding signal in case of North Indian polyphonic music and detecting tāla using the parameters of NIMS rhythm, has been clearly discussed.
• A large number of polyphonic music samples from Hindi vocal songs from bhajan or devotional, semi-classical and filmy genres were analyzed for studying the effectiveness of the proposed new method.
• The experimental result of the present investigation clearly supports the pronounced effectiveness of the proposed technique.
• We would extend this methodology for studying other features (both stationary and non-stationary) of the all the relevant tāla-s of NIMS and designing an automated rhythmwise categorization system for polyphonic compositions. This system may be used for content-based music retrieval in NIMS. Also a potential tool in the area of music research and training is expected to come out of it.
• Limitations of the method are that it cannot distinguish between tāla-s of same mātra. For example deepchandi and dhamar tāla-s have number of mātra -s, bol-s and beats in a cycle. We plan to extend this elementary model of tāladetection system for all the NIMS tāla-s, by including other properties like timbral information and nonlinear properties of different kinds of tablā strokes/bol-s. We may also attempt to transcript the tāla-bol-s in a polyphonic composition. This extended version of the model may address the NIMS tāla-s which share same mātra and also have variety of lay-s.
The initial version of the software version of the proposed algorithm is in Talman, where users can upload relevant .wav files of a polyphonic song played on NIMS tāla-s and find out the tāla computationally.
Acknowledgement
We thank the Department of Higher Education and Rabindra Bharati University, Govt. of West Bengal, India for logistics support of computational analysis. We also thank renowned musician Subhranil Sarkar for helping us to annotate test data, validate test results and Shiraz Ray (Deepa Ghosh Research Foundation) for extending help in editing the manuscript to enhance its understandability.
References
- London J (2004) Hearing in Time. Oxford University Press.
- Cooper GW, Meyer LB (1960) The rhythmic structure of music.
- Lerdahl F, Jackendoff RS (1985) A Generative Theory of Tonal Music. Cambridge, Mass.: MIT Press Ltd, p. 384.
- Latham A (2011) The Oxford Companion to Music. Oxford University Press.
- Gillet O, Richard G (2005) Extraction And Remixing Of Drum Tracks From Polyphonic Music Signals, in Applications of Signal Processing to Audio and Acoustics. IEEE Workshop, pp. 315-318.
- Ono N, Miyamoto K, Roux JL, Kameoka H, Sagayama S (2008) Separation of a monaural audio signal into harmonic/percussive components by complementary diffusion on spectrogram, in Proc. of the EUSICO European Signal Processing Conf.
- Clayton M (2000) Time in Indian Music?: Rhythm , Metre and Form in North Indian Rag Performance. Oxford University Press.
- Courtney DR (2000) Fundamentals of Tabla. (4th editn) Sur Sangeet Services, pp. 294.
- Naimpalli S (2005) The theory and Practice of TABLA. Popular Prakashan, Mumbai, India, pp. 250.
- Alghoniemy M, Tewfik AH (1999) Rhythm and periodicity detection in polyphonic music. In: IEEE Third Workshop on Multimedia Signal Processing. IEEE, pp. 185-190.
- Rosenthal D (1992) Emulation of Human Rhythm Perception. Comp Music J 16: 64-76.
- Bakhmutova IV, Gusev VD, Titkova TN (1997) The Search for Adaptations in Song Melodies. Comp Music J 21: 58-67.
- Todd NPM, Brown GJ (1996) Visualization of Rhythm, Time and Meters. Art Intel Rev 10: 99-119.
- Foote J (2000) Automatic audio segmentation using a measure of audio novelty. IEEE International Conference on Multimedia and Expo, Tokyo, Japan, pp. 452-455.
- Klapuri AP, Eronen AJ, Astola JT (2006) Analysis of the meter of acoustic musical signals. IEEE Trans Audio Speech Lang Proc 14: 342-355.
- Gouyon F, Herrera P (2003) Determination of the meter of musical audio signals: Seeking recurrences in beat segment descriptors, 114th Audio Engineering Society Convention Spain, pp. 5811
- Bhat R (1991) Acoustics of a cavity-backed membrane: The Indian musical drum. J Acous Soc Ame 90: 1469-1474.
- Goto M, Muraoka Y (1995) A real-time beat tracking system for audio signals. In Proc. International Computer Music Conference Japan, pp. 311-335
- Scheirer ED (1998) Tempo and beat analysis of acoustic musical signals. J Acoust Soc Am 103: 588-601.
- Gouyon F, Herrera P (2001) Exploration of techniques for automatic labeling of audio drum tracks instruments. Curr Direct Comp Music.
- Dixon S (2007) Evaluation of The Audio Beat Tracking System BeatRoot. J New Music Res 36: 39-50.
- Davies MEP, Plumbley MD (2007) Context-dependent beat tracking of Musical Audio. IEEE Trans Audio Speech Lang Proc 15: 1009-1020.
- Böck S, Schedl M (2011) Enhanced Beat Tracking with Context-aware Neural Networks. Proc 14th Int Conf Digital Audio Effects pp. 135-139.
- Raman CV (1921) On some Indian stringed instruments. Proc Indian Assoc Cultiv Sci 33: 29-33.
- Malu S, Siddharthan A (2000) Acoustics of the Indian drum. ArXiv Preprint Math 1-13.
- Patel A D, Iversen JR (2003) Acoustic and Perceptual Comparison of Speech and Drum Sounds in the North Indian Tabla Tradition: An Empirical Study of Sound Symbolism. 15th ICPhS Barcelona, pp, 925-928.
- Rae A (2009) Generative Rhythmic Models.
- Gulati S, Rao V, Rao P (2011) Meter detection from audio for Indian music in Proc. Int. Symposium on Computer Music Modeling and Retrieval pp. 34-43.
- Schuller B, Eyben F, Rigoll G (2007) Fast and Robust Meter and Tempo Recognition for the Automatic Discrimination of Ballroom Dance Styles. In Acoustics, Speech and Signal Processing, 2007 IEEE International Conference pp 217-220.
- Miron M (2011) Automatic Detection of Hindustani Talas.
- Bhaduri S, Saha SK, Mazumdar C (2014) Matra and Tempo Detection for INDIC Tala-s. Adv Com Inf, Proceedings of the Second International Conference on Advanced Computing, Networking and Informatics 1: 213-220.
- Bhaduri S, Saha SK, Mazumdar C (2014) A Novel Method for Tempo Detection of INDIC Tala-s. Fourth Int Conf Emerg App Inf Tech 222-227.
- Bhaduri S, Das O, Saha SK, Mazumdar C (2015) Rhythm analysis of tabla signal by detecting the cyclic pattern. Innovations Syst Softw Eng 11:187-195.
- Maity A, Pratihar R, Mitra A, Dey S, Agrawal V et al (2015) Multifractal Detrended Fluctuation Analysis of alpha and theta EEG rhythms with musical stimuli. Chaos Solitons Fractals 81: 52-67.
- Clayton M (1997) The meter and the tāl in the music of north india. Tradit Music 10: 169-189.
- Uhle C, Dittmar C, Sporer T (2003) Extraction of drum tracks from polyphonic music using Independent Subspace Analysis. In Proceedings of the 4th International Symposium on Independent Component Analysis and Blind Signal Separation, pp. 843-848.
- Helen M, Virtanen T (2005) Separation of drums from polyphonic music using non-negative matrix factorization and support vector machine. Proc. Eur Signal Process Conf.
- Zils A, Pachet F, Delerue O, Gouyon F (2002) Automatic extraction of drum tracks from polyphonic music signals. Web Delivering of Music, WEDELMUSIC, Proceedings Second International Conference, pp. 179-183.
- Yoshii K, Goto M, Okuno HG (2004) Automatic drum sound description for real-world music using template adaptation and matching methods. In Proceedings of the International Conference on Music Information Retrieval, pp. 184-191.
- Gillet O, Richard G (2003) Automatic Labelling of Tabla Signals. In Proc. ISMIR.
- Moore BCJ, Glasberg BR (1983) Suggested formulae for calculating auditory-filter bandwidths and excitation patterns. The J Aco Soc Ame 74: 750-753.
- Ranade SG (1964) Frequency spectra of Indian music and musical instruments.Research Department, All India Radio, New Delhi.
- Lartillot O, Toiviainen P (2007) A matlab toolbox for musical feature extraction from audio. International Conference on Digital Audio. pp. 1-8.

Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences