ISSN : 2349-3917
American Journal of Computer Science and Information Technology
Deployment of Soft-Computing for System Computing and Informatics
Ashit Kumar Dutta*
Department of Computer Science, Shaqra University, Saudi Arabia
- *Corresponding Author:
- Dutta AK
Department of Computer Science, Shaqra University, Saudi Arabia
E-mail: drashitkumar@yahoo.com
Received date: March 14, 2018; Accepted date: March 31, 2018; Published date: April 06, 2018
Citation: Dutta AK (2018) Deployment of Soft-Computing for System Computing and Informatics. Am J Compt Sci Inform Technol Vol.6 No.2:18 doi: 10.21767/2349-3917.100018
Copyright: © 2018 Dutta AK. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Intuitionistic fuzzy (IFuzzy) have remarkable applications in complex real world problems. Fuzzy set is the superset of IFuzzy, many applications have been successfully implemented in the field of computer science. Soft computing is related to the system finds solution for the vague problems, introduced in early 90’s and became popular by its approach to the real world problem. The development of IFuzzy leads to improvement in softcomputing method to analyze the complex system with complex inputs. It is possible to build a hybrid intelligent system using IFuzzy methods. The proposed study has derived IFuzzy methods for reliability problems in the soft computing and some definitions for the complex problems.
Keywords
Fuzzy set; Intuitionistic fuzzy set; Decisionpair; IFuzzy; Dfuzzy; System Reliability
Introduction
In a real world, there will be a situation to handle uncertainty, imprecision and vagueness. Complex data in the field of economics, engineering, medical science are having kind of uncertainty. All the existing mathematical tools for modeling, reasoning and calculation are deal with certain problems, they are not able to solvemore complex problems in real life situations. Many researches are evolved to handle the complexity of uncertain data. There are a wide range of applications are availed through fuzzy set theory, rough set and Intuitionistic fuzzy. Many flaws are there in the existing methods and could not find solution for the reliability of the system. The existing methods lacks in efficiency to express the uncertainty parameters to solve vagueness found in the system. The basic theory of soft sets can well deal with uncertain, fuzzy, unclear and vague data. This theory shows its effectiveness in many different fields such as the Smoothness of functions, Game theory, Operations research, Riemann integration, Perron integration, Probability theory, and Measurement theory.
This paper generalizes intuitionistic fuzzy soft set. The paper is organized as follows: Section 2 review the existing literature in Intuitionistic fuzzy soft set and relevant definitions used in the proposed work. In section 3 discuss the definitions of intuitionistic fuzzy sets and define some operations such as subset, union, intersection, compliment all explained with examples. In section 4 discuss about the proposed research for system reliability. The section-5 conclude the paper with a future scope of the research.
Review of Literature
Fuzzy-reliability is an application introduced in systems engineering as fuzzy sets has the ability to find uncertain and ambiguous information. Existing models are handling only precise data. There will be so many reasons for the degradation of Systems because they experience component failures typically have many degrees of "working" between their "fully working" and "fully not-working" states. Fuzzy theory provides a solution for such systems with the association of the system’s degree of working with an element’s degree of membership in a set [1-10]. The proposed study present a soft-computing method for system reliability applying the intuitionistic fuzzy theory of Atanassov [1-3]. Maji et al. [4] used soft set in decision making problem. Chen proposed a reasonable definition of parameter reduction of soft sets and improved the application of a soft set in a decision making problem. An attempt to assess sound quality based on soft set approach has been made by Bozenakostek. Maji et al. [5] introduced several algebraic operations in soft set theory and published a detailed theoretical study on soft sets. The same authors [3] also extended crisp soft sets to fuzzy soft sets. The algebraic nature of soft set has been studied by several researchers [6-25]. Aktas and Cagman [26] initiated soft groups, Feng [27] defined soft semirings. Sun [8] introduced a basic version of soft module theory, which extends the concept of a module by including some algebraic structures in soft sets. Gohel et al. [12] developed a security model in Big data. The research has explained the methods to defend and protect the big data. The research will be useful for the proposed research to enhance its features.
Fundamentals of IFS
Let us have a fixed universe E. Let A be a subset of E. Let us construct the set
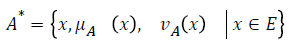
Where 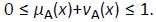 We will call the set A* intuitionistic fuzzy set (IFS).
We will call the set A* intuitionistic fuzzy set (IFS).
In the publications on IFS authors mainly deal with the concept of intuitionistic fuzzy set A* rather than with fixed set A. To simplify the complexity, use notation A instead of A*.
Mathematically, a more precise definition of the IFS is the following:
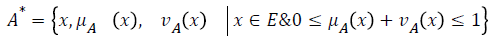
but it is also more complex one and never used, as of 2008 [3].
Functions μA:E → (0,1) and vA:E→(0,1) represent degree of membership (validity, etc.) and non-membership (nonvalidity, etc.). Also defined is function πA:E → (0,1) through
π(x)=1-μ(x)-v(x), corresponding to the degree of uncertainty (indeterminacy, etc.)
Obviously, for every ordinary fuzzy set A:πA(x)=0 for each x E
Definition 1 and these sets have the form 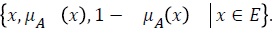
Let be a set called a universe of discourse. An intuitionistic fuzzy set (IFS), A in E is an object of the form
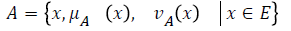
Where μA and vA are functions given by
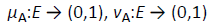
Satisfying the constraint 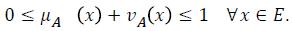 The quantities μA(x) and vA(x) are called, respectively, the “degree of membership” and the “degree of non-membership” of the element x, to the set A. The amount A(x)=1-μA-vA(x) is the “indeterministic part” of the evaluation for membership or non-membership status of the element x in . This part remains indeterministic due to the hesitation of the decision-maker. Hesitation is a part and parcel of the human decision-making process. It varies from man to man, agent to agent. Even for a fixed agent, hesitation varies in different situations. In fact, hesitation is almost unavoidable in all human-centered systems. In fuzzy set theory, this hesitation is assumed to be nil. As a result, if the membership value of an element is decided, its non-membership value is also, by definition, determined. If an element of hesitation exists in the mind of the decision-maker, fuzzy set theory is not appropriate. In such a case IFS theory plays a dominant role to the decision-makers or problem analysts.
The quantities μA(x) and vA(x) are called, respectively, the “degree of membership” and the “degree of non-membership” of the element x, to the set A. The amount A(x)=1-μA-vA(x) is the “indeterministic part” of the evaluation for membership or non-membership status of the element x in . This part remains indeterministic due to the hesitation of the decision-maker. Hesitation is a part and parcel of the human decision-making process. It varies from man to man, agent to agent. Even for a fixed agent, hesitation varies in different situations. In fact, hesitation is almost unavoidable in all human-centered systems. In fuzzy set theory, this hesitation is assumed to be nil. As a result, if the membership value of an element is decided, its non-membership value is also, by definition, determined. If an element of hesitation exists in the mind of the decision-maker, fuzzy set theory is not appropriate. In such a case IFS theory plays a dominant role to the decision-makers or problem analysts.
Definition 2
If A and B are two intuitionistic fuzzy subsets of the set E, then
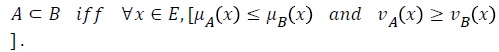
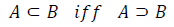
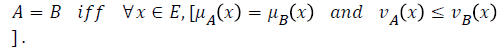
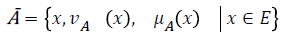
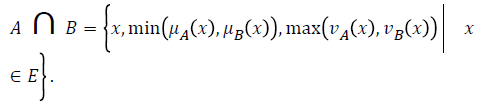
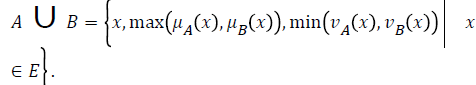
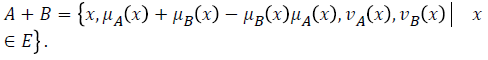
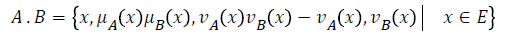
System Reliability
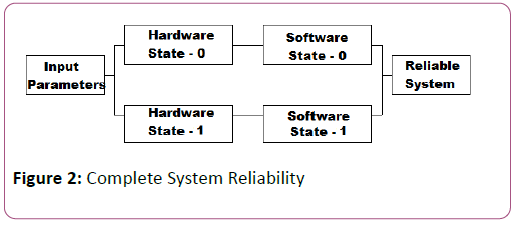
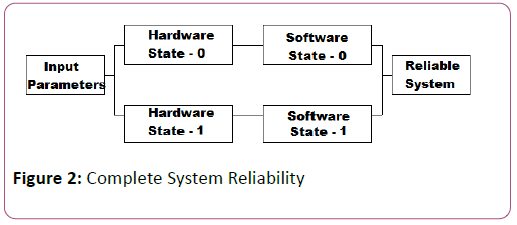
The Figure 1 illustrates the detailed block diagram of the system. This system consists of some input parameters which receives the system attribute then converts it to a data stream suitable for the processing of the Ifuzzy. The reliable system will be the output of the system. The active parameters of complex system acts as the input, while the concrete parameters of the system will be ignored as the data. Ifuzzy monitors the sanity of the active process of the reliability of the system. The output from the two parallel connected states of the system is combined and processed by the Ifuzzy and generated as the reliable output. If the system is not reliable then the input parameters will be modified and the process will be repeated again to get the reliable system.
Input and output are passive devices with IFuzzy control. The system deals with real-time operating system and vague system. The system stays completely operational as long as at least one state is in operation.
The hardware and software have been modelled as two distinct entities. The software and the hardware are operating in series as the process cannot function if the hardware or the software is not operational (Figure 2).
Figure 2: Model Architecture
The two states (software+hardware) combine together to form a complex system. Within the complex system, the two states are placed in parallel as the system can function when one of the states fails to execute the operation.
The input parameters, the complex system and the output have been placed in series as failure of any of the three parts will lead to complete failure of the system.
Availability of individual components
This section will discuss about the computing of the availability of individual components. ATBF (Average time between failure) and ATTR (Average time to repair) values are estimated for each component. For hardware components, ATBF information can be obtained from hardware manufactures data sheets. If the hardware has been customized by the user, then the hardware group would provide ATBF information for the board. ATTR estimates for hardware are based on the degree to which the system will be monitored by operators. Here the estimation for the hardware ATTR to be around 2 h.
Once ATBF and ATTR are known, the availability of the component can be calculated using the following formula:
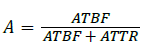
Estimating software ATBF is a Complex task. Software ATBF is really the time between subsequent reboots of the software. This interval may be estimated from the defect rate of the system. The estimate can also be based on previous experience with similar systems. Here we estimate the ATBF to be around 4000 h. The ATTR is the time taken to reboot the failed processor. Our processor supports automatic reboot, so we estimate the software ATTR to be around 5 min. Note that 5 min might seem to be on the higher side. But ATTR should include the following:
• Time wasted in activities aborted due to software crash.
• Time taken to detect failure of the system.
• Time taken by the failed processor to reboot and come back in service.
Things to note from the above table are (Table 1):
| Components | ATBF (Hours) | ATTR (Hours) | Availability (%) |
|---|---|---|---|
| Input Parameters | 100000 | 2 | 99.998 |
| Hardware | 10,000 | 2 | 99.98% |
| Software | 2190 | 5 (Minutes) | 100.00% |
| Output | 1,00,000 | 2 | 100.00% |
Table 1: Availability of components
Availability of individual components
This section will discuss about the computing of the availability of individual components. ATBF (Average time between failure) and ATTR (Average time to repair) values are estimated for each component. For hardware components, ATBF information can be obtained from hardware manufactures data sheets. If the hardware has been customized by the user, then the hardware group would provide ATBF information for the board. ATTR estimates for hardware are based on the degree to which the system will be monitored by operators. Here the estimation for the hardware ATTR to be around 2 h.
Once ATBF and ATTR are known, the availability of the component can be calculated using the following formula:
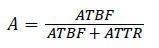
Estimating software ATBF is a Complex task. Software ATBF is really the time between subsequent reboots of the software. This interval may be estimated from the defect rate of the system. The estimate can also be based on previous experience with similar systems. Here we estimate the ATBF to be around 4000 h. The ATTR is the time taken to reboot the failed processor. Our processor supports automatic reboot, so we estimate the software ATTR to be around 5 min. Note that 5 min might seem to be on the higher side. But ATTR should include the following:
• Time wasted in activities aborted due to software crash.
• Time taken to detect failure of the system.
• Time taken by the failed processor to reboot and come back in service.
Things to note from the above table are (Table 1):
• Availability of software is higher, even though hardware ATBF is higher. The main reason is that software has a much lower ATTR. In other words, the software does fail often but it recovers quickly, thereby having less impact on system availability.
• The input parameters and output have fairly high availability, thus fairly high availability can be achieved even without redundant components [11-19].
System availability
This section will discuss the computing of the availability of the entire system. These calculations have been based on serial and parallel availability calculation formulas (Table 2).
| Components | Availability (%) | Downtime |
|---|---|---|
| Software & Hardware | 99.98% | 2.08 h/year |
| System in parallel | 100.00% | 3.15 sec/year |
| Reliable System | 100.00% | 21.08 min/year |
Table 2: System Availability
Example:
Consider an IFuzzy q=“expecting more profit”. Suppose that aowner propose the following IFuzzyQ for the IFuzzyq (without any hesitation or indeterministic-value in Q):-
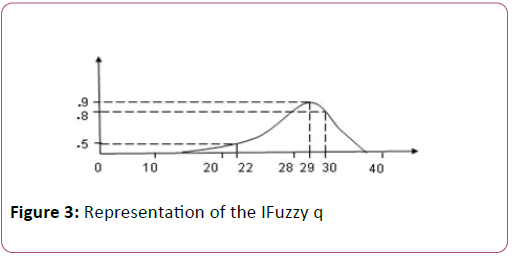
For the decision-pair (.5, .8), the (.5, .8) Representation of the IFuzzy q is 22, 29, 30),.9, .1. In this case, the (.98, .96) representation of the IFQ q will be denoted by the notation < (□, 29, □), .9, .1>, where □ is the don’t-care symbol. But, in our work in the subsequent sections we will not consider such type of situations (involving □), because an intelligent-agent is expected to choose the decision-parameters (α,ß) in such a way that the constraint α,ß ≤ μx (m) holds. (In this example, it is the constraint α,ß ≤ μx (29)).
In our work in this paper, we will present a method of softcomputing for large-system reliability. As a reliability engineer, we frequently say, for instance, that a system is 90% reliable during the time period (t1,t2). Consequently, in our intuitionistic fuzzy computing, we choose the universe of discourse U to be the unit interval (0,1), instead of the set R of real numbers [20-26]. Our basic assumptions in our technique of reliabilitycomputation are that (Figure 3):
Figure 3: Model Architecture
• The membership-function and non-membership function are triangular in diagrams. The (α,ß representation in this case will be called to be (α,ß triangular representation.
• There exists a point x õ (0,1) on the left-side of the triangle, at which μ(x)=0 and v(x)=1. (If there are more than one such points, we take sup of them).
• There exists a point y õ (0,1) on the right-side of the triangle, at which μ(x)=0 and v(x)=1. (If there are more than one such points, we take inf of them).
Definition IFuzzy and DIFuzzy
Consider a component P of a large complex system S, whose reliability is not known but could be imprecisely estimated as an IFQ r. Such type of imprecise estimate of reliability is called intuitionistic fuzzy reliability or IFR (in short).
Let an intelligent agent propose the IFuzzy R for the IFuzzy r. Suppose that the (0,0) triangular representation of the IFR r is <(a,b,c),μr(b),vr(b)>. Then this representation of the reliability r in a (0,0) triangular fashion is called to be the IFuzzification of the IFR [27].
The concept of DIFuzzy is explained below by an example.
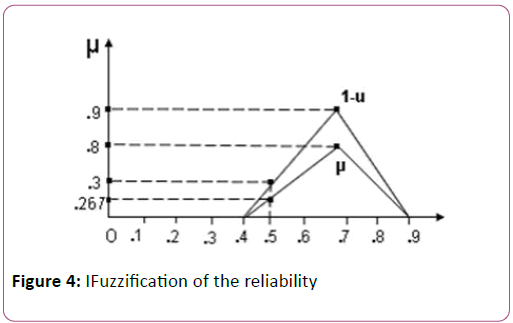
Example: Let a component P of a system S has the reliability r=”approximately 8”. Suppose that an intelligent decision-maker proposes an IFS R for this IFQ r given by:
Here we see that the IFuzzification of the reliability “approximately 7” is the tuple <(.4, .7, .9), .8, .1>. If it is de- IFuzzified, it signifies the following results (Figure 4):
• Reliability of the component is .7 with minimum membership value .8 and maximum membership value .9.
• Reliability of this component cannot be .4 or less, in any case.
• Reliability of this component cannot be .9 or more, in any case.
• Reliability can only be in the open interval (.4, .9); For instance, reliability could be .5 with minimum membership value=.267 and maximum membership value=.3.
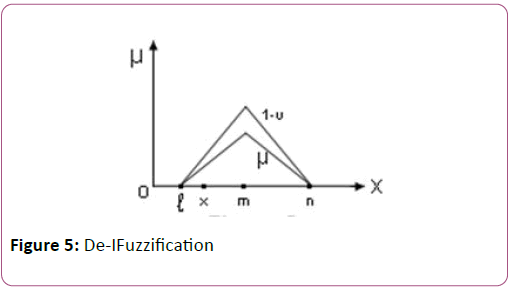
Now, consider a general case of IFuzzification as shown below:
Let, IFuzzyof a reliability IFuzzy r be given by the tuple < (l,m,n), μr (m), vr (m) >. De-IFuzzification of this tuple reveals the following results (Figure 5):
• Reliability of the component is m with minimum membership value μr (m) and maximum membership value 1- vr (m).
• Reliability of this component cannot be l or less
• Reliability of this component cannot be more than n.
Real time examples
The proposed research is used to implement efficient automated systems like hand written recognition system, and complex image recognition system. The complex image recognition system will be useful to detect mass and other unidentified diseases in the human brain. The proposed research has proved that can be implemented in fuzzy systems.
Conclusion
In this paper, we have reported a method of soft-computing of reliability of a complex system under intuitionistic fuzzy situation. Reliability has an inverse relation with real-time and also with the incorporation of more number of components in the configuration of the system. Our method will be useful if the data are of IF nature. In case all the indeterministic parts are nil although the computation, the method reduces to a fuzzy computing technique of system reliability. Our method of fuzzycomputing, so developed as a special case of IF-computing, is a simple for computation and is different from the fuzzycomputing of reliability suggested in [7,11,13,17,21,22]. We have introduced the IFuzzification and De-IFuzzification of imprecise data for reliability-analysis, and we have described our technique of soft-computing by using (0,0) triangular representation of IFR. We have defined (α,ß representation of an IFQ, of which a special case is the (0,0) triangular representation.
References
- Atanassov K (1986) Intuitionistic fuzzy sets. Fuzzy Sets and Systems 2087- 2096.
- Atanassov K (1999) Intuitionistic Fuzzy Sets: Theory and Applications, Physica- Verlag, Heidelberg.
- Atanassov K (1989) More on Intuitionistic Fuzzy Sets. Fuzzy Sets and Systems 33: 37-46.
- Maji PK, Roy AR, Biswas R (2003) Soft set theory, Computers and Mathematics with Applications 45: 555-562.
- Maji PK, Bismas R, Roy AR (2001) Fuzzy soft set theory. J Fuzzy Mathematics 3: 589-602.
- Bertolini M, Bevilacqua M, Mason G (2004) Reliability Design of Industrial Plants using Petri Nets in Proceedings of the Asian International Workshop (AIWARM 2004) on Advanced Reliability Modeling, Hiroshima, Japan 33-40.
- Biswas R (1996) Similarity measurements in IFS. Notes on IFS 2: 5-14.
- Sun QM, Zhang ZL, Liu J (2008) Soft sets and soft modules, Rough Sets and Knowledge Technology 5009: 403-409.
- Bowles JB, Pelaez CE (1995) Application of fuzzy logic to reliability engineering, Proceedings of the IEEE 435-449.
- Cai KY (1996) Introduction to Fuzzy Reliability, Kluwer Academic Publishers, Dordrecht.
- Cai KY, Wen CY (1990) Street-lighting lamps replacement: a fuzzy viewpoint, Fuzzy Sets and Systems 37: 161-172.
- Gohel HA, Upadhyay H (2018) Developing Security Intelligence in Big Data. In: Margret Knowledge Computing and Its Applications. Springer, Singapore.
- Cai KY, Wen CY, Zhang ML (1991) Fuzzy reliability modeling of gracefully degradable computing systems. Reliability Engineering and system safety 33: 141-157.
- Cai KY (1996) System failure engineering and fuzzy methodology: An introductory overview. Fuzzy sets and systems 83: 113-133.
- Rotshtein A (2007) Fuzzy reliability analyses of human's algorithms activity. Reliability 21: 3-18.
- Rotshtein A (2011) Fuzzy-algorithmic analysis of complex systems reliability.Cybernetics and Systems Analysis 47: 919-931.
- Glushkov VM (1965) Automata theory and formal microprogram transformations. Cybernetics 1: 1-8.
- Katelnikov DI, Rotshtein AP (2010) Fuzzy algorithmic simulation of reliability: control and correction resource optimization. J Comp Sys Sci Int 49: 967-971.
- Kolarik WJ, Woldstad JC, Lu S, Lu H (2004) Human performance reliability: on-line assessment using fuzzy logic. IIE Transactions 36: 457-467.
- Zou FZ, Li CX (2001) Chaotic model for software reliability. Chinese J Comp 24: 281-291.
- Dick S, Bethel CL, Kandel A (2007) Software-reliability modeling: the case for deterministic behaviour. IEEE Transactions on Systems, Man, and Cybernetics Part A 37: 106-119.
- May RM (1976) Simple mathematical models with very complicated dynamics. Nature 261: 459-467.
- Kozlov BM, Ushakov IA (1975) Handbook on Reliability of Radio and Automation Systems. Soviet Radio, Moscow, Russia.
- Gen M, Cheng R (1997) Genetic Algorithms and Engineering Design. John Wiley & Sons.
- Molodtsov D (1999) Soft set theory-first results. Computers and Mathematics with Applications 37: 19-31.
- Aktas H, Cagman N (2007) Soft sets and soft groups. Information Science 177: 2726-2735.
- Feng F, JunYB, Zhao XZ (2008) Soft semirings Computers and Mathematics with Applications 56: 2621-2628.

Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences