ISSN : 2349-3917
American Journal of Computer Science and Information Technology
Convergence Analysis of Acceleration Schemes: Spectral Radius versus Condition Number
S Azizu*
Department of Mathematics, Wenchi Methodist Senior High School, Wenchi, Ghana
- *Corresponding Author:
- S. Azizu
Department of Mathematics, Wenchi Methodist Senior High School, Wenchi, Ghana
E-mail: abdulaziz_seidu@rocketmail.com
Received date: January 17, 2018; Accepted date: January 23, 2018; Published date: January 29, 2018
Citation: Azizu S (2018) Convergence Analysis of Acceleration Schemes: Spectral Radius versus Condition Number. Am J Compt Sci Inform Technol 6:1. doi: 10.21767/2349-3917.100013
Copyright: © 2018 Azizu S. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The theory of matrix splitting plays an important role in convergence analysis for the acceleration schemes. Spectral radius allows us to make a complete description of eigenvalues of a matrix and is independent of any particular matrix norm. The aim of this research article is to find the relationship between spectral radius and condition number in terms of stability of algorithms using various classes of linear systems and determine whether the condition number can be used to predict the convergence of acceleration schemes as well as iterative methods in the solutions of systems of linear equation. From the results obtained using matlab programming language, there is strong relationship between spectral radius and condition number for dense symmetric positive definite (SPD) and tridiagonal system. The relationship is shown as k(A)=||A|| ||A-1||=ρ(A)(A-1) and the value of condition number helps to predict the rate of convergence and iterations for a given linear system.
Keywords
The theory of matrix splitting plays an important role in convergence analysis for the acceleration schemes. Spectral radius allows us to make a complete description of eigenvalues of a matrix and is independent of any particular matrix norm. The aim of this research article is to find the relationship between spectral radius and condition number in terms of stability of algorithms using various classes of linear systems and determine whether the condition number can be used to predict the convergence of acceleration schemes as well as iterative methods in the solutions of systems of linear equation. From the results obtained using matlab programming language, there is strong relationship between spectral radius and condition number for dense symmetric positive definite (SPD) and tridiagonal system. The relationship is shown as k(A)=||A|| ||A-1||=ρ(A)(A-1) and the value of condition number helps to predict the rate of convergence and iterations for a given linear system.
Introduction
One of the fundamental building blocks of numerical computing is the ability to solve linear system. Systems of linear equations may consist of two or more linear equations. A solution exists for it if and only if the solution satisfies all equations of the system [1-7]. A System of linear equations has the general form:
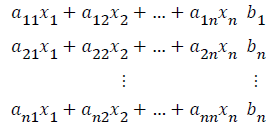
Where xj(j=1,2,…,n) are unknown variables, aij(i,j=1,2,…,n) are the coefficients, and bi(i=1,2,…,n) are right hand side (RHS) constants A system of linear equation in n variables is a set of n equations with each equation being linear in n variables. It is generally denoted by the equation Ax=b, where A is a square matrix, x unknown vector and a known vector. A solution is a set of numerical values x1,x2,x3,….,xn that satisfies all the equations [7]. Various methods have been introduced to solve systems of linear equations. There is no single method that is best for all situations. These methods should be determined according to speed and accuracy. The methods for systems of linear equations can be divided into two groups: Direct and Iterative Methods. The approximate methods that provide solutions for systems of linear equations are called iterative methods. They start from an initial guess and improve the approximation until an absolute error is less than the pre-defined tolerance.
Related Works
In linear system, the restarted acceleration scheme without using Chebyshev polynomial to work as the acceleration process for stationary iterative methods has been studied [6]. Refinement after a fixed number of iteration and the improved approximate was applied using both inner and outer loops to obtain more accurate approximation. According to [7] when the basic iteration matrix is similar to a diagonal matrix and all eigenvalues are real and lie in the interval [a,b], the Chebyshev extrapolation scheme for SOR employs the Chebyshev polynomials, where D=nonsingular diagonal matrix (A) and λ=eigenvalue of A. An important number of applications in science and engineering require the numerical solution of large nonsymmetric matrix for eigenvalue problem [5] that involved computing the problem of eigenvalue.
Concept of Condition Number on Linear Systems
The conditioning of a problem is a measure of how sensitive the problem is to small perturbations in the data. Condition number of matrix is a measure of stability or sensitivity of the matrix to numerical operations [2]. The condition number of a problem measures the sensitivity of the solution to small changes in the input [1]. When a system has a low condition number, it implies well-conditioned while high condition number is regarded as ill conditioned. The condition number is symbolically written as:
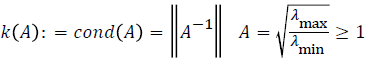
Convergence of Stationary Iterative methods
The necessary and sufficient condition for convergence of the Jacobi method is that matrix A is strictly diagonally dominant, then for any choice of x(0), both the Jacobi methods give sequences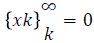 that converge to approximate solution of linear system.
that converge to approximate solution of linear system.
The method is an improved version of the Jacobi method. It is defined on matrices with non-zero diagonals, but convergence is only guaranteed if the matrix is either diagonally dominant, or symmetric and (semi) positive definite. If a linear system has strictly dominant coefficient matrix and each equation is solved for each strictly dominant variable then, the Gauss-Seidel iteration will converge to for any choice of x0 [4].
If the relaxation parameter ω=1 the SOR method is equal to the Gauss-Seidel method. The SOR method fails to converge if is outside the interval (0, 2). In general, it is not possible to compute in advance the value of that will maximize the rate of convergence of SOR.
Spectral Radius
The spectral radius of an n × n matrix A is ρ(A)=max|λ| =limn→∞||An||1/n where λ is an eigenvalue of A. The theory of matrix splitting plays an important role in convergence analysis for the iterative Scheme. The concept of spectral radius allows us to make a complete description of eigenvalues of a matrix and is independent of any particular matrix norm. Consider the linear system Ax=b for the iterative solution of systems of linear equations, it is customary to represent the matrix A as A=MN: If the matrix M is nonsingular, the iterative method is expressed in the form xk+1=M-1Nxk+M-1b; which converges to the unique solution x=A-1b of the system Ax=b for each initial vector x(0) if, and only if, ρ(M-1N)<1, where ρ(M-1N) is the spectral radius of the iteration matrix (M-1N).
The Chebyshev extrapolation algorithm is as follows:
• Input the coefficient matrix A, initial guess x0 and the RHS vector b and set maximum value for iteration.
• Set the tolerance, ε=0.0001
• Compute the residual vector r=b-Ax0
• Compute z=M/r
• Compute the error vector
• Stop if error<ε
Accelerate Gradient acceleration scheme improves the convergence stationary iterative methods for solving a large and sparse system. Accelerated gradient schemes applied the idea of initial vector for the iterative scheme [3].
The Accelerated gradient algorithm is as follows:
• Let x0 õ Rn and y0=x0 and θ0=1k ≥ 0
• Compute 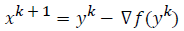
• Compute 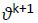
• Compute 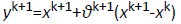
Numerical Experiment
In the numerical, we present some numerical results to show the relationship between spectral radius and condition number in relation to the convergence of acceleration schemes. The algorithms were ran using MATLAB software version 7.0.1 on Intel(R) Pentium (R) CPU P600 @ 1.87GHz 1.87 and Installed Memory (RAM): 4.00GB for dense, Tridiagonal and dense SPD. From the dense system in Table 1, there is no relationship between condition number and spectral. Again, for dense SPD and tridiagonal system, the relationship is shown as k(A)=||A|| ||A-1||=ρ(A)(A-1).
| Classes of System | Cond B | Spectral B | ||A|| ||A-1|| | Ρ(A)(A-1) |
|---|---|---|---|---|
| Dense n=3 | 7.6775 | 16.874 | 7.6775 | 7.2702 |
| Dense n=4 | 9.3496 | 22.8987 | 9.3496 | 6.805 |
| Dense n=5 | 12.5361 | 28.311 | 12.5361 | 8.1889 |
| Dense SPD n=5 | 2.6655 | 13.3279 | 2.6655 | 2.6655 |
| Dense SPD n=9 | 3.7346 | 33.6121 | 3.7346 | 3.7346 |
| Dense SPD n=20 | 6.361 | 127.2287 | 6.361 | 6.361 |
| Tridiagonal n=3 | 1.7888 | 6.4142 | 1.7888 | 1.7888 |
| Tridiagonal n=20 | 2.3087 | 6.9777 | 2.3087 | 2.3087 |
| Tridiagonal n=30 | 2.322 | 6.9897 | 2.322 | 2.322 |
Table 1: Classes of systems and Analysis
Conclusion and Future Work
The spectral radius often determines convergence of iterative schemes for linear systems and is related to condition number as k(A)=||A|| ||A-1||=ρ(A)(A-1) for Tridiagonal system and dense SPD system. Numerical experiment was carried using matlab programming software. Future work is to consider Richardson acceleration scheme for specific banded system.
References
- Kenney CS, Laub AJ (1994) Small-Sample Statistical Condition Estimates for General Matrix Functions. SIAM J Sci Comput 15: 36-61.
- Merhdoust F (2010) A randomized algorithm for estimating the condition number of Matrices 204-210.
- Auslender A, Teboulle M (2006) Interior gradient and proximal methods for convex and conic Optimization. SIAM J Opt 16: 697-725.
- Jamil N (2012) A Comparison of Direct and Indirect Solvers for Linear Systems of equations. Int J Emerg Sci 2: 310-321.
- Saad Y (1984) Acceleration Techniques for Solving Nonsymmetric Eigenvalue problem. Math Comput 42: 567-588.
- Peng W, Lin Q (2012) An acceleration method for stationary iterative solution of linear System of equation. J Adv Appl Math Mech 4: 473-482.
- Duan L, Zheng B (2008) Chebyshev polynomial acceleration of SOR solving the rank of Deficient linear system. Sci Paper 1-16.

Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences
