ISSN : 2573-4466
Insights in Enzyme Research
Biocatalytic Activity of Mushroom Tyrosinase in Ionic Liquids: Specific Ion Effects and the Hofmeister Series
Mark P Heitz*, Jason W Rupp and Kim W Horn
Department of Chemistry and Biochemistry, The College at Brockport, SUNY 228 Smith Hall, 350 New Campus Drive, Brockport, New York, 14420, USA
- *Corresponding Author:
- Mark P Heitz
Department of Chemistry and Biochemistry
The College at Brockport, SUNY 228 Smith Hall
350 New Campus Drive, Brockport, New York, 14420, USA
Tel: 585-395-5586
E-mail: mheitz@brockport.edu
Received date: January 30, 2018; Accepted date: February 22, 2018; Published date: March 01, 2018
Citation: Heitz MP, Rupp JW, Horn KW (2018) Biocatalytic Activity of Mushroom Tyrosinase in Ionic Liquids: Specific Ion Effects and the Hofmeister Series. Insights Enzyme Res. Vol.2 No.1:12. doi: 10.21767/2573-4466.100012
Copyright: © 2018 Heitz MP, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
We report results on the correlation between mushroom tyrosinase inhibition kinetics and ionic liquid (IL) ion effects predicted by the Hofmeister series. A spectrophotometric assay was used to measure product formation from which we extracted the kcat and Km kinetic parameters. The kcat/Km ratio was calculated for both the neat buffer solution and IL-modified solution, which allowed us to determine the relative enzymatic activity. The results show that tyrosinase activity was inhibited by the presence of IL ions. Consistent with Hofmeister predictions, the more kosmotropic cations and chaotropic anions had the greatest inhibition effect. Both ion identity and concentration contributed to overall observed relative activity change in the systems studied here, with an overall range of relative activity change from ~1.0 to ~0.15 depending on the specific ions used. [Im21 +] [NO3 -] showed the least effect on tyrosinase activity over a wide concentration range (20–150 mM) compared to when using an IL with a more chaotropic anion, [Im21 +] [Tf2N-], where the enzyme activity was ~0.2 at all concentrations studied between 20-80 mM. The inhibitory effect of [Tf2N-] was quite significant. We also observed low relative activities (~0.15) in IL solutions that used increasingly kosmotropic cations, [Im41 +] [Cl-] and [Im61 +][Cl-]. Again, concentration worked in parallel with specific ion identities and the less kosmotropic cation [Im41 +] required higher concentrations (~80 mM, [Im41 +] [Cl-]) to achieve the same level of inhibition as only 40 mM of [Im61 +] [Cl-]. The Hofmeister series for both cations and anions used here appears to be a good predictor of inhibition in our IL solutions. In addition, a reliable measure of inhibition also followed increased anion hydrophobicity and polarizability.
Keywords
Imidazolium; Ionic liquid; Inhibition; Tyrosinase; L-dopa; Biocatalysis; Hofmeister series
Introduction
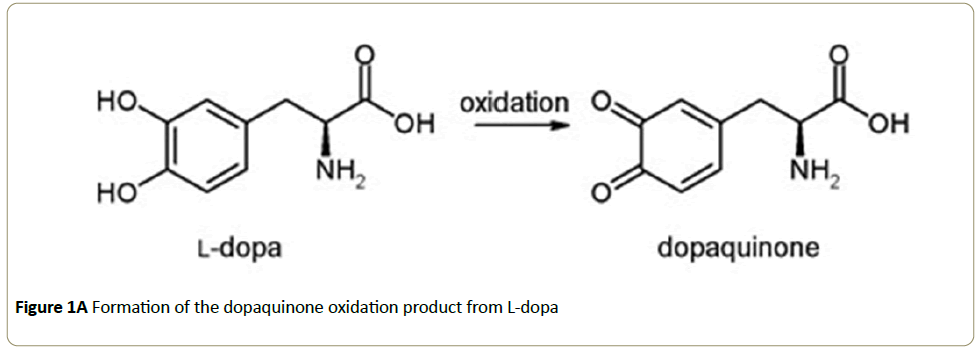
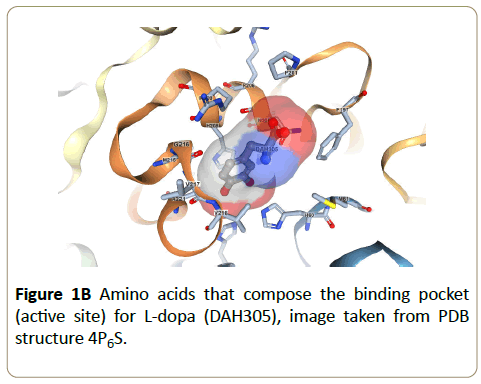
The enzyme tyrosinase, found in melanocytes, plays an important role in the biosynthesis of melanins and other polyphenolic compounds [1]. Melanocytes are cells found in the basal layer of the epidermis and are key in the production of melanin, the pigmentation molecule responsible for skin color and protection of skin cells and DNA from UV damage [2]. Melanin is synthesized by tyrosinase and its formation is rate-limited by the enzymatic reaction. Even when melanocytes become cancerous the melanoma can still produce melanin and it is of interest to note that the elevated expression of the tyrosinase is found in melanoma cells [3] and that the control of in vivo melanin production is regulated by the inhibition of tyrosinase activity [4-7]. Moreover, previous research highlights that a strategy of targeting with inhibitors can be used to treat melanogenic disorder [4,5,7]. Thus, understanding inhibitors effects and how tyrosinase is influenced can have a significant impact on the diagnosis and treatment of melanin related diseases. Another important application of tyrosinase chemistry is that it plays a key role in the browning of fruit skin. As a result, the agricultural and food industries are continually seeking ways to reduce the impact of food waste and are interested in identifying tyrosinase inhibitors as a way to prevent over riping of fruit [8,9]. The clear advantage of governing tyrosinase chemistry in this application is increased product shelf life with the potential to effectively increase agricultural yields while simultaneously reducing the economic impact of waste. Tyrosinase is known to catalyze the hydroxylation of phenolic substrates to catechol derivatives, which in turn are able to further oxidize into orthoquinone products [6,7,10,11]. Active sites are enzyme specific and structurally the tyrosinase active site is reported to consist of two oxygen-bridged Cu2+ ions bound to six histidines through electrostatic and cation-π interactions [9,12]. Figure 1 shows the chemical structures for the tyrosinase-catalzyed oxidation of L-dopa to dopaquinone. The tyrosinase catalytic mechanism for the conversion of L-dopa has been described in detail [9,12] and the importance of the histidine-rich copper centers facilitates the necessary proton transfer sites. The ribbon structure of tyrosinase with L-dopa incorporated in the active site is shown in Figure 1 and can be accessed through the RCSB protein data bank, structure 4P6S [13].
As a class, ionic liquids (ILs) are thought to be environmentally friendly solvents, because of favorable properties such as low volatility. The IL physicochemical properties can be fine-tuned simply by choosing specific combinations of cations and anions. Miscibility of many ILs with aqueous media may make them potentially good candidates for biocatalytic reactions [14-21]. Agricultural applications of ILs have been studied because of their antimicrobial properties [22] and for potential use in herbicidal applications [23], including imidazolium ILs. When incorporated into an enzyme, ILs have been reported to have mixed effects on activity. In some cases ILs can enhance enzymatic activity and selectivity as highlighted in a recent mini-review by Goldfeder and Fishman [24]. In contrast, the IL cations and anion can disrupt the amino acid interactions and alter the enzyme conformation through alteration of the hydrophobic effect (which governs secondary and tertiary protein structure), hydrophobic hydration, surface tension, and water-water interactions among other factors, all of which induce a corresponding diminution of enzymatic activity [25]. Typically, these structural changes cause disruption to the enzyme’s active site and performance can be compromised [18,26]. Thus, the ability to predict the effect of ILs on activity is important. A large number of reports have demonstrated that activity effects in many IL systems can be predicted by the Hofmeister series, wherein the relative kosmotropicity (ordermaking or structure-making) or chaotropicity (disordermaking) of the IL ions dictate the outcome of enzymatic activity, particularly in bulk aqueous solutions where the IL ions tend to be solvent separated [27,28]. Kosmotropes are ions that tend to be small and highly charged, which results in strong ion-water interactions that exceeds that of water-water hydrogen bonding interactions. The overall solution entropy is lower because of the increased organization around the hydrated ion. Thus, charge density is a key factor in considering Hofmeister effects. Conversely, chaotropes are large ions with a low charge density and weak hydration characteristics. For these ions there is a net increase in solution entropy because of weaker ion-water interactions. These general effects have been discussed at length in several good reviews [24-26,28-32]. However, we hasten to point out that more recently it has been suggested that the hydrogenbonded bulk water interactions (i.e., Hofmeister effects) may not be the optimal perspective with which to view the influence of IL ion-protein interactions because interpretations based on this effect is at best imprecise [33]. Rather, the focus may be better placed on local enzyme-water-ion interactions, non-electrostatic interactions, and ion polarizabilites [34].
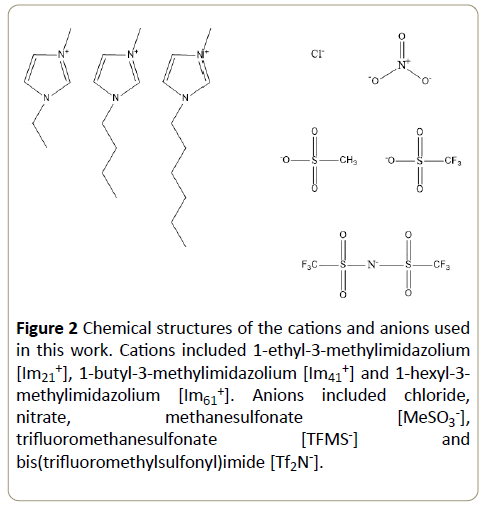
The literature contains the availability of only rudimentary data on the Hofmeister effects that stem from IL ions. In order to systematically assess Hofmeister predictions for tyrosinase with respect to cation and anion effects of imidazolium ILs, we measured the reaction kinetics between mushroom tyrosinase and L-dopa in the presence of the seven imidazolium-based ionic liquids, shown in Figure 2. These imidazolium ILs were selected primarily because of their favorable miscibility with aqueous solutions. We studied the effect of IL cation hydrophobicity by increasing the alkyl chain substituent to determine its impact on enzymatic activity. To elucidate the effect of anion, we selected the [Im21+] cation to use with several anions anticipating that [Im21+] would have simultaneously the highest solubility and the weakest direct impact on the enzyme hydrophobic interactions. In the presence of [Im21+] the anion effect on the resulting enzyme stability and activity should be most clearly delineated. Since anions are reported to have the greater impact on activity and stability [26,33], we were particularly interested to determine the effects of ion hydrophobicity, polarizability, anion size and degree of fluorination on the tyrosinase activity.
Figure 2: Chemical structures of the cations and anions used in this work. Cations included 1-ethyl-3-methylimidazolium [Im21+], 1-butyl-3-methylimidazolium [Im41+] and 1-hexyl-3-methylimidazolium [Im61+]. Anions included chloride, nitrate, methanesulfonate [MeSO3-], trifluoromethanesulfonate [TFMS-] and bis(trifluoromethylsulfonyl)imide [Tf2N-].
Materials and Methods
Mushroom tyrosinase (50K units) and L-3,4- dihydroxylphenylalaine (L-dopa, 98%) were purchased from Sigma-Aldrich. Ionic liquids were purchased as follows: 1- ethyl-3-methylimidazolium nitrate ([Im21+][NO3-], 97%) was from Fluka; 1-ethyl-3-methylimidazolium methanesulfonate ([Im21+][MeSO3-], 98%), 1-ethyl-3-methylimidazolium trifluoromethanesulfonate ([Im21+][TFMS-], 98%), 1-ethyl-3- methylimidazolium bis(trifluoromethylsulfonyl)imide ([Im21+] [Tf2N-], 98%), and 1-butyl-3-methylimidazolium chloride ([Im41+][Cl-], 98%) were all from EMD; 1-butyl-3- methylimidazolium methanesulfonate ([Im41+][MeSO3-], 95%) was from IoLiTec; and 1-hexyl-3-methylimidazolium chloride ([Im61+][Cl-], 97%) was from Solvent Innovation.
pH and ionic strength were controlled using a 50 mM phosphate buffer solution adjusted to pH=6.8. A tyrosinase concentration of 52 nM was used in all experiments, which was determined by performing a series of independent experiments to find the concentration that closely reached Vmax. Enzyme solutions were prepared by massing an appropriate quantity of tyrosinase and dissolving in 100 mL of buffer using a volumetric flask. Freshly prepared solutions were the afternoon prior to use and equilibrated and stored overnight at 4°C. Typically, only enough solution was prepared so that it was consumed after no more than two to three days of use. To minimize any photolytic side reactions, the volumetric flask was wrapped tightly in aluminum foil to protect the solution from ambient light. Similarly, the L-dopa solutions were prepared at a concentration of 1.5 mg/mL Ldopa and prepared using the same protocol as tyrosinase solutions. Enzyme, substrate, and buffer solutions were always stored in the absence of light at 4°C when not in use. Ionic liquids were stored in a desiccator when not in use.
The reaction between tyrosinase and L-dopa was determined by tracking the formation of dopaquinone, the Ldopa oxidation product (see Figure 1), using a Perkin-Elmer Lambda 800 UV/VIS Spectrometer set at 475 nm. During experiments, the enzyme and substrate solutions were placed in a sand bath kept at 35°C to maintain equilibration prior to measurement. Reactions were carried out in a quartz cuvette by directly micropipetting solutions into the cuvette, shaking for 2 sec and placing immediately into the spectrometer. A blank solution composed of buffer and ionic liquid was used for correcting the measured absorbance. IL solution concentrations were prepared by micropipetting the appropriate amount to prepare the desired solution concentration. Inclusive of all systems measured here, the IL concentrations ranged from as low as about 5 mM to upwards of 150 mM IL.
Absorbance data were analyzed using the method of initial rates to extract the initial reaction velocity by calculating the change in absorbance during the first minute of reaction. The data were scrutinized over several time window ranges to choose a time range that insured a linear absorbance response. The resulting kinetic data was analyzed using the Michaelis-Menten kinetic model, by applying the Lineweaver- Burk (L-B, double reciprocal) method to create plots as
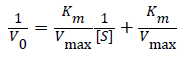 (1)
(1)
Where V0 is the initial reaction velocity calculated from the absorbance versus time data, Km is the Michaelis constant, Vmax is the maximum reaction velocity, and [S] is the substrate concentration [35]. Fits to the data by a linear model allowed extraction of the slope (=Km/Vmax), y-intercept (1/Vmax), and x-intercept (=-1/Km). Then, assuming a two-step kinetic model, the product formation rate constant (k2) was assumed to be the limiting rate constant of the enzyme-catalyzed reaction (kcat), where Vmax=k2[E] and [E] is the enzyme concentration [35]. Using these recovered parameters we calculated the ratio. We normalized the IL data by acquiring the kinetics for two sets of solutions, the IL solution itself and the buffer solution that was used to prepare the specific IL solution, to calculate the relative activity ratio,
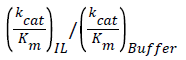 (2)
(2)
with which we could evaluate directly the ILs effects on the reaction.
Results and Discussion
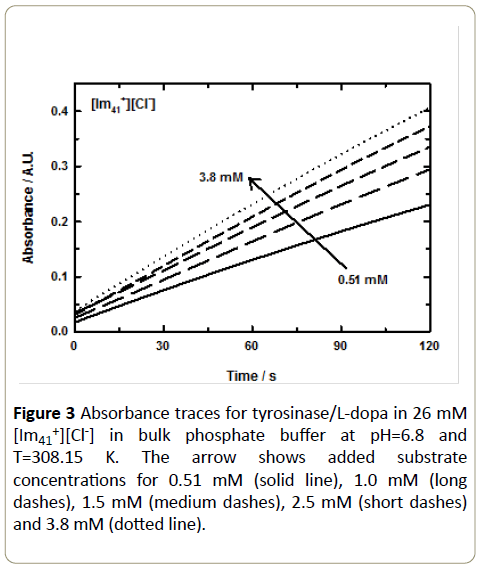
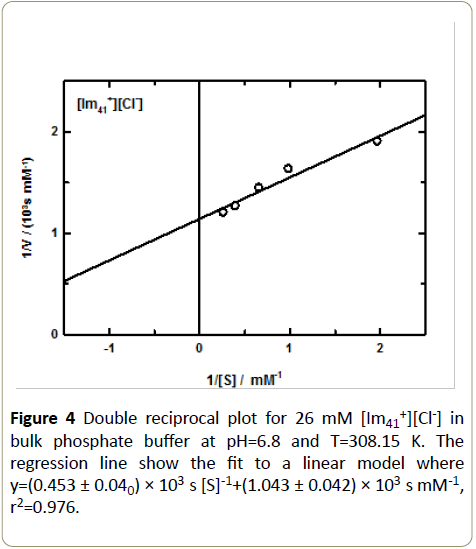
The time course of absorbance was measured at 475 nm for a set of up to six L-dopa concentrations to produce a complete data set. Figure 3 presents an example set of absorbance data for 26 mM [Im41+][Cl-] in a bulk phosphate buffer at T=308.15 K and pH=6.8. The substrate volume was varied from 0.5-3.8 mM. These traces are representative for all of the IL/enzyme/ substrate systems studied here. Figure 4 shows an example of
Figure 4: Double reciprocal plot for 26 mM [Im41+][Cl-] in bulk phosphate buffer at pH=6.8 and T=308.15 K. The regression line show the fit to a linear model where y=(0.453 ± 0.040) × 103 s [S]-1+(1.043 ± 0.042) × 103 s mM-1,r2=0.976.
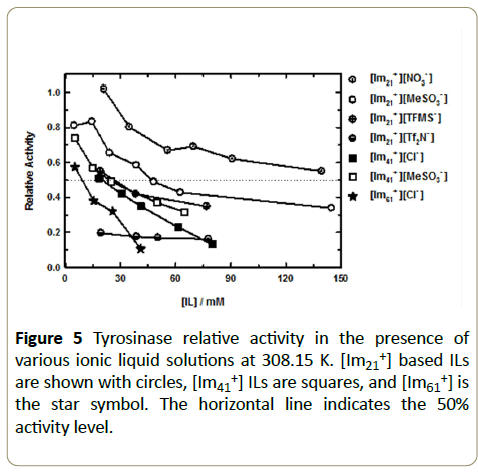
The L-B (double reciprocal) plot that resulted the reaction of tyrosinase/L-dopa in a 26 mM [Im41+][Cl-]/phosphate buffer solution at pH=6.8 and T=308.15 K. As expected, the data were well described by a linear fit, r2~0.98. L-B plots are used to reveal the effects of inhibitors on enzymatic reactions, including the identification of inhibition type (competitive, non-competitive, etc.) [35]. We have reported the details of our inhibition calculations for these imidazolium ILs with tyrosinase, along with a complete set of molecular docking calculations elsewhere [36]. Figure 5 collects the resulting relative activities determined in this way as a function of the amount of IL. Without exception the data show that for any cation/anion combination selected the relative enzymatic activity consistently decreased with increased amounts of IL. On closer inspection, the data reveals that the relative activity follows a predictable dependence on the chemical structure of the cation and anion. Our data shows that the relative activity is dependent on the cation’s alkyl chain length and that an increase from C2 to C6 results in a significant increase of the IL inhibitory effect on tyrosinase activity. At a constant IL concentration, this behavior is generally independent of the associated anion (for example, see Figure 5 at 30 mM IL) and is particularly noticeable when the anion identity is held constant ([MeSO3-], open circle and square symbols and [Cl-], completely filled square and star symbols). We observed that at about 15-18 mM IL, the relative tyrosinase activity decreased by roughly 25% for Cl- when comparing [Im41+] [Cl-] to [Im61+] [Cl-], a trend that repeats for [Im21+] [MeSO3-] and [Im41+] [MeSO3-] solutions at 25 mM IL. On increasing the amount of [MeSO3-] in solution to 65 mM IL we see a more substantial drop in activity approaching about 50%. This clearly shows that relative enzymatic activity decreases as the imidazolium cation alkyl chain length increases and that relative activity diminishes with larger amounts of these ILs. We associate these observations with the increased hydrophobic effect of the cation as carbon chain length increases. Our data using tyrosinase/IL solutions agrees with the observations of Yang et al. who also reported decreased enzyme activity for penicillium expansum lipase in the presence of imidazolium ILs. Further, based on other literature discussions our results are also consistent with the idea that increasing the kosmotropicity of the imidazolium cation ([Im21+] [Im61+]) should yield decreased stability and enzyme functionality [26,29,32,37,38,39]. Indeed, tyrosinase activity is diminished in the expected cation order [Im21+]>[Im41+]>[Im61+] and we hypothesize that the reasons stem from at least three likely contributions. First, van der Waals interactions (that vary in proportion to cation’s hydrophobic character) between tyrosinase and the longer chain cations increase and thus displace water from the protein’s hydration layer. Simultaneously, the increased hydrophobic interactions induce stronger water-water associations therefore the pattern here is consistent with Hofmeister trends [25,26,28]. Additionally, it is reasonable to assume that there are associated structural changes upon this type of enzyme/IL association. Therefore, a second effect is that cations with longer chains intercalate into the enzyme’s structure perturbing the secondary and tertiary structures that result in a denaturing of the enzyme, much like a typical surfactant molecule [25,26,40]. Third, the isoelectric point of tyrosinase is 4.5 [41] and thus under our experimental conditions in phosphate buffer at pH=6.8 tyrosinase has a net negative surface charge. This in turn further concentrates [Imx1+] at the enzyme interface and the result is an increased probability of cation association, not only with the enzyme surface but also with the enzyme’s active site [24,26,40].
The sole exception to the observed cation pattern for these enzyme/IL systems occurs with [Im21+][Tf2N-]. We point out that [Im21+] is considered to be a weakly chaotropic cation [28] and that [Tf2N-] is a chaotropic anion, the combination of which should have a mixed effect on enzymatic activity [26,32]. From a Hofmeister perspective, a chaotropic cation should favor stability and activity because of lower hydrophobicity and therefore tendency to promote a watermaking structures resulting from ion hydration and thus ultimately enhancing the enzyme’s hydrophobic effect whereas a chaotropic anion through its high polarizability and low water affinity tends to weaken the hydrophobic effect and enhances entropic conformational change. Other factors also contribute to the overall observed ion effects such as ion affinity for water, surface tension effects, active site flexibility, and specific ion effects all of which complicate the data interpretation. Using only our present data we cannot differentiate between the various contributions. However, for example we note that the [Im21+] [Tf2N-] ions have significantly different affinities for water and for [Tf2N-] the presence of accessible, strongly hydrophobic amino acids in tyrosinase’s active site (such as alanine, valine, methionine, see Figure 1) increases the driving force for [Im21+] [Tf2N-] to separate. This, coupled with additional support from hydrogen-bonding amino acids in the active site (as offered by histidines, see Figure 1) suggests that the enzyme readily accommodates this anion. Our recent molecular docking studies suggested that both [Im21+] and [Tf2N-] preferentially locate in the tyrosinase active site [36]. As a result of the favorable interactions between tyrosinase and [Im21+] [Tf2N-] the association equilibrium constant for this IL should be small, and therefore the number of ions in solution large, with the end result that the overall effect of each ion is maximized. This would explain the observed activity, which shows [Im21+] [Tf2N-] has a strongly deleterious effect on the tyrosinase activity. Moreover, since in general anions have a more active role in enzyme (de-)stabilization through greater polarizability effects relative to cations [26,42], it is not surprising that [Im21+] [Tf2N-] destabilizes tyrosinase to a much larger extent than the other [Im21+] ILs.
While the influence of [Imx1+] cations on tyrosinase activity is driven by the hydrophobic effect through the carbon chain length variation, the effect of anions is more diverse. The anion influence was assessed by examining anion size (volume and ellipsoid radius), polarizability, degree of fluorination, and tendency toward hydrogen bonding. To help isolate the anion effect and minimize added contributions from the cation structure, we measured several anions using [Im21+]. When considering only these ILs we noted that the tyrosinase relative activity decreased in order of [NO3-]>[MeSO3-]>[TFMS-]>[Tf2N-]. In an effort to describe this observation we used Spartan16® [43] to compute volume, radius, polarizability, and solvent accessible surface area for each anion used in this work using a polarizable continuum water model to mimic the bulk aqueous phase. Except for molecular mechanics and semi-empirical models, the calculation methods used in Spartan have been documented [44]. In this work, all calculations were performed at the Hartree-Fock 3-21G level of theory for ions in water using the SM8 [45] water model. The SM8 water model is an implicit solvation model that estimates the electrostatic polarization of a continuous medium using bulk solvent properties. We also used DFT theory with the B3LYP functional and 6-31G* basis set, which yielded hydrated ion energies that were <1% different than the HF 3-21G method so a more sophisticated level of theory was not needed for our purposes here. Table 1 summarizes the computed data and we note several features from these data. The computed volumes provide a good correlation to the relative activity suggesting that one cursory metric to correlate relative activity for these systems is anion volume. Figure 5 (circles) shows that for the [Im21+] ILs, it is [NO3-] that had the smallest impact on the tyrosinase relative activity response consistent with it being the smallest anion. At 20 mM IL the [NO3-] solution yields essentially the same kinetics as the reaction in buffer solution and upon increasing IL concentration the relative activity still remains high at >100 mM IL, decreasing by roughly 45% over the IL range studied here. However, a more reliable correlation between relative activity and anion chaotropicity is seen by the change in anion solvation free energy, see Table 1, which shows that [NO3-] is the most hydrophilic anion of this group.
| Anion | Volume/Å3 | Ovality | Radius / Å | Polarizability | Solvent Accessible Surface Area, Å2 | Enthalpy kJ·mol-1 | Entropy J·mol-1·K-1 | Gibbs Energy kJ·mol-1 |
|---|---|---|---|---|---|---|---|---|
| [Cl-] | 23.7 | 1.00 | 1.7 | 36.6 | 51.4 | -457.6 | 161.6 | -457.6 |
| [NO3-] | 41.1 | 1.13 | 2.1 | 41.1 | 56.2 | -277.4 | 256.3 | -277.4 |
| [MeSO3-] | 69.9 | 1.17 | 3.3 | 42.7 | 73.9 | -658.4 | 288.2 | -658.5 |
| [TFMS-] | 83.6 | 1.22 | 3.7 | 43.6 | 73.3 | -953.5 | 346.7 | -953.5 |
| [Tf2N-] | 153.8 | 1.43 | 7.3 | 49.7 | 103.4 | -1812 | 483.7 | -1812 |
| L-Dopa | 187.6 | 1.35 | 10.1 | 53.7 | 147.6 | -697.0 | 479.4 | -697.0 |
Table 1: Computed Anion Parameters.1. Parameters are computed using Wave function’s Spartan16® [43] at 298.15 K using the SM8 water parameterization to represent the experimental aqueous phase. 2. Volumes are calculated from a space-filling (CPK) model. 3. Ovality Represents deviation from spherical as the ratio of ellipsoid axes. 4. Radius is estimated by measuring the distance across the minimized geometry between atoms at the distal ends of the structure. 5. Accessible surface area of an electron density surface where “surface” is defined by an electron density of 0.002 electrons/au3 and accessible corresponds to a probe with a 1 Å radius. 6. L-dopa is included for comparison.
In correspondence with a description of enzyme activity that follows the Hofmeister series, we also calculated the anion polarizability in a water dielectric continuum using the SM8 water model in Spartan®. Accordingly, Table 1 collects the computed results for the polarizability and shows that the values systematically increase. The effect of electrostatic polarization by each of these anions becomes clear and provides a basis for understanding why these anions become more increasingly chaotropic toward tyrosinase. We tabulated the calculated entropy and see that it too systematically increases for this set of anions, to the point where [Tf2N-] shows the same value as L-dopa. For the anions used here, the molecular structure reveals an implicit connection to the polarizability through the influence of anion fluorination. With [TFMS-] and [Tf2N-], the number of fluorine atoms increases and it is these two anions that yield the lowest relative activity. The [Im21+] [Tf2N-] relative activity is diminished substantially, by about 80% compared to neat buffer, even with only about 20 mM IL added to solution. Thus, one means by which one can assess the anion chaotropicity is by evaluating an ion’s hydrophobicity. Our results show a consistent correlation between anion hydrophobicity and a decreased relative activity for tyrosinase. Another computed parameter that we considered was the anion’s accessible surface area. [Tf2N-] shows a considerable increase in surface area compared to the other ions used here owing to its larger size. For [Tf2N-], this parameter is on par with that of L-dopa. Along with an increased solvent accessible surface area comes the increased probability that the extent of anion/enzyme interactions will be greater and thus perturb the tyrosinase conformation, offering another point that supports the observed increase in inhibition behavior. From the above results and observations, we can state that in solutions formed by using the [Im21+] cation paired with the set of anions studied here the inhibition of the tyrosinase/L-dopa reaction appears to reasonably follow the predictions based on the Hofmeister rules for enzyme activity.
In addition to indicators of chaotropicity such as solvation energy and polarizability, we find that in the systems presented here the IL concentration also contributes to the change in relative activity. The concentrations used in this work (<200 mM IL) were chosen to minimize the potential for IL aggregation. Critical micelle concentrations (CMC) of several imidazolium bromide ILs in aqueous solution were reported to have CMC values of ~2 to 170 mM as carbon chain length decreased from C14 to C8 [46], which is generally representative of the imidazolium ILs as a class. Therefore, in this work we expect that for C2 to C6 imidazolium ILs studied the CMC has not been exceeded so that the ILs exist as solvent separated ions. Moreover, the ILs used vary in their relative hydrophobicity with [NO3-] as the more hydrophilic anion compared to [Tf2N-], which is more strongly hydrophobic. Thus, the degree of hydrophobicity may also play a role in the degree of IL dissociation and therefore the concentration of free ions in solution. So in addition to the parameters discussed above, electrostatic interactions can also be considered as a driver of the extent to which tyrosinase is destabilized. We note that each of the IL/tyrosinase systems show the same general trend, where increasing the IL concentration decreases the tyrosinase relative activity. The main difference is the extent to which the specific anions affect the relative activity. Our data suggest several correlations that include simple measures such as size to anion polarization. While [MeSO3-] is more similar to [NO3-] in size, [TFMS-] and [Tf2N-] are approximately 2 and 4 times larger, respectively, and with this increase in anion size the relative activity drops significantly even at the smallest IL concentration values (see [Im21+] data at 20 mM), Figure 5. For the larger anions, the charge density is decreased and so electrostatic interactions presumably have a less prominent role in reducing activity. In addition to simple anion volume, we also tabulated the degree to which each of these anions is non-spherical, as reported by the ovality. An ovality value of 1.00 represents a shape that is perfectly spherical and deviations from 1.00 are an indication of the anion becoming increasingly ellipsoidal. Given the molecular structure, we see that [Tf2N-] has the most ellipsoidal shape with a semi-axis ratio of about 1.4. Using the measuring tool in Spartan® we estimated the major axis to be 7.3 Å so not only is [Tf2N-] voluminous but it is also dimensionally the longest anion and approaches the length of L-dopa (10.1 Å). It is interesting to note that the given each of the size related parameters the [Tf2N-] anion has the greatest effect on tyrosinase activity. It appears that anion size (and associated charge density) offers an appealing, simple, intuitive correlation to describe the chaotropicity and hence the measured relative activity in the tyrosinase/L-dopa system. We recently performed molecular docking studies for each of the IL ions used here and in summary those results showed that the cations all localized exclusively in the tyrosinase active site, whereas the anion results were more varied [36]. For example, [NO3-] dockings were associated with residues that were outside of the active site, which suggests that electrostatic interactions play a more significant role for ILs with this anion. On the other hand, the more hydrophobic [Tf2N-] docking results all showed preferential binding in the enzyme active site. So, although electrostatic interactions between IL ions and tyrosinase do play a role in the overall enzymatic activity, from these data alone we cannot assign relative contributions to each effect. However, based on our data here and the docking simulation results it does appear that electrostatics do not exclusively determine enzymatic stabilization or activity in the tyrosinase/L-dopa reaction and that other parameters also must be considered [25,33,34].
One final comparison that can be made from this data is by more closely examining the [Im41+] and [Im61+] cation solutions. In these cases, we used ILs that were based on the Cl- ion. With the Cl- anion, [Im61+] clearly has a more substantial effect compared to [Im41+]. Not only are the cations increasingly hydrophobic and therefore more kosmotropic [25,33,47,48], but combined with the hardness of Cl- is apparently a particularly potent combination to diminish enzymatic activity. This is made apparent by comparing the two [Im41+] ILs. When [Im41+] is paired with Cl- there is a greater effect on relative activity over [MeSO3-], although one might expect the reverse behavior if the size difference or polarizability alone is considered. This trend also appears to be opposite to what would be predicted based on Hofmeister arguments since Cl- is typically reported as an activating ion [25,28,32,33,42,47]. Among all of the competing effects such as ion pair structure, ion size, hydrophobicity, and polarizability (in effect charge density) it is difficult to pinpoint one measure that reliably predicts all IL behaviors. However, in agreement with previous work [33] it does appear that polarization effects are the more important contributions and is the better criterion to use in assessing enzymatic stabilization. One possible explanation as to why Cl- is more destabilizing than [MeSO3-] may lie in the size “advantage” of Cl- which allows it to penetrate into the active site where it can directly interact with the Cu2+ ions that regulate the enzymatic activity [12,13].
Conclusion
Tyrosinases are enzymes that have a principal role in melanin biosynthesis and are important because they are responsible for controlling skin and hair pigmentation in mammals. In this work we focused on the type 3 [13] coppercontaining oxidase mushroom tyrosinase. We have characterized the enzymatic activity of this enzyme using the substrate L-dopa in phosphate buffer solution at pH=6.8 and in buffer solutions that in turn included the presence of one of seven alkylimidazolium ionic liquids. Using the Michaelis- Menten kinetic parameters to determine the enzymatic activity, we calculated the relative activity as the ratio of (activity in the presence of ILs) / (activity in buffer).
Our experimental results clearly showed increased inhibition of the tyrosinase activity in the presence of aqueous based solutions of the [Imx1+] ILs. Relative activity exhibited a pronounced decrease with increasing length of the cation’s alkyl chain substituent (increasing kosmotropicity) in the sequence [Im21+]>[Im41+]>[Im61+], consistent with literature reports [25,27,33,47,48]. The observed behavior is clearly connected to the increased cation hydrophobicity. We observed increased inhibition as the anion was varied in proportion to increasing size and polarizability. The extent of halogenation, as it governs anion polarization changes, also offers a convenient characterization of the experimental anion order. From the anion results with the [Im21+] cation, the increasing inhibition trend was found to be [NO3-]<[MeSO3-]<[TFMS-]<[Tf2N-]. Our data further showed that although the Cl- anion is usually viewed as an activitystabilizing anion, when paired with the kosmotropic cations [Im41+] and [Im61+] the cation effect seems to play a more dominant role in the overall inhibition of tyrosinase. Given the progressions in the anion properties that were reported in Table 1, with particular attention to the hydration energies and ion polarizability coupled with the hydrophobicity of the cations used here, a somewhat mixed effect on tyrosinase activity. One further point bears mention here. We point out that from this present data alone, we were unable to fully deconvolute the individual ion effects for a specific IL. For example, while [Im21+] was used as a “constant” against which we could evaluate anion contributions, chosen because it was the least perturbing cation, it nonetheless contributed to some fraction of activity decrease. That is, we have not yet been able to quantify the degree to which any one specific ion, anion or cation, either offsets or enhances the activity. However, what was made clear is that regardless of the particular ion pairings, all imidazolium ILs resulted in decreased enzymatic activity. Our goal at the outset was to evaluate the applicability of Hofmeister rules for imidazolium IL effects on tyrosinase activity. We can conclude that from these measurements that the cation/anion effects are in good agreement with trends predicted by the Hofmeister series, and the series does offer a predictive means of assessing the impact of imidazolium ILs on tyrosinase activity. This conclusion is not a general result and additional systematic measurements using a wide range of enzyme systems will be required before we can fully describe and understand the impact and interplay of ILs in enzymatic reactions.
Acknowledgements
The authors gratefully acknowledge support from The College at Brockport, SUNY through the scholarly incentive and Provost post-tenure grant programs.
Conflict of Interest
The Author(s) declare(s) that there is no conflict of interest.
References
- Korner A, Pawelek J (1982) Mammalian Tyrosinase Catalyzes Three Reactions in the Biosynthesis of Melanin. Science 217: 1163-1165.
- Gilchrest BA, Blog FB, Szabo G (1979) Effects of Aging and Chronic Sun Exposure on Melanocytes in Human Skin. J Invest Dermatol 73: 141-143.
- Kim TI, Park J, Park S, Choi Y, Kim Y, et al. (2011) Visualization of Tyrosinase Activity in Melanoma Cells by a BODIPY-Based Fluorescent Probe. Chem Commun 47: 12640-12642.
- Sánchez-Ferrer A, Rodriguez-Lopez JN, Garcia-Canovas F, Garcia-Carmona F (1995) Tyrosinase: A Comprehensive Review of its Mechanism. Biochim Biophys Acta 1247: 1-11.
- Jones K, Hughes J, Hong M, Jia Q, Orndorff S, et al.(2002) Modulation of Melanogenesis by Aloesin: a competitive Inhibitor of Tyrosinase. Pigment Cell Res 15: 335-340.
- Hearing VJ, Jimenez M (1987) Mammalian tyrosinase-The critical regulatory control point in melanocyte pigmentation. Int J Biochem 19: 1141-1147.
- Ando H, Kondoh H, Ichihashi M, Hearing VJ (2007) Approaches to Identify Inhibitors of Melanin Biosynthesis via the Quality Control of Tyrosinase. J Invest Dermatol 127: 751-761.
- Lin YF, Hu YH, Lin HT, Liu X, Chen YH, et al. (2013) Inhibitory Effects of Propyl Gallate on Tyrosinase and Its Application in Controlling Pericarp Browning of Harvested Longan Fruits. J Agric Food Chem 61: 2889-2895.
- Lerch K (1995) Tyrosinase: Molecular and Active-Site Structure. Enzymatic Browning and Its Prevention. ACS Symposium Series, vol. 600, American Chem Society, pp: 64-80.
- Battaini G, Monzani E, Casella L, Lonardi E, Tepper A.W.J.W, et al. (2002) Tyrosinase-Catalyzed Oxidation of Fluorophenols. J Biol Chem 277: 44606-44612.
- Germanas JP, Wang S, Miner A, Hao W, Ready JM, et al. (2007) Discovery of Small-Molecule Inhibitors of Tyrosinase. Bio org, Med Chem Lett 17: 6871-6875.
- Olivares C, Solano F (2009) New Insights into the Active Site Structure and Catalytic Mechanism of Tyrosinase and its Related Proteins. Pigment Cell Melanoma Res 22: 750-760.
- Goldfeder M, Kanteev M, Isaschar-Ovdat S, Adir N, Fishman A, et al. (2014) Determination of Tyrosinase Substrate-Binding Modes Reveals Mechanistic differences Between Type-3 Copper Proteins. Nat Commun 5: 4505.
- Stein F, Kragl U (2014) Biocatalytic Reactions in Ionic Liquids. Ionic Liquids Further UnCOILed. pp. 193-216.
- Kragl U, Eckstein M, Kaftzik N (2003) Biocatalytic Reactions in Ionic Liquids. Ionic Liquids in Synthesis, vol 1 pp: 336-347.
- Xu P, Zheng GW, Du PX, Zong MH, Lou WY et al. (2016) Whole-Cell Biocatalytic Processes with Ionic Liquids. ACS Sustainable Chem Eng 4: 371-386.
- Egorova KS, Gordeev EG, Ananikov VP (2017) Biological Activity of Ionic Liquids and Their Application in Pharmaceutics and Medicine. Chem Rev 117: 7132-7189.
- Sun J, Liu H, Yang W, Chen S, Fu S (2017) Molecular Mechanisms Underlying Inhibitory Binding of Alkylimidazolium Ionic Liquids to Laccase. Molecules 22: 1353.
- Jha I, Kumar A, Venkatesu P (2015) The Overriding Roles of Concentration and Hydrophobic Effect on Structure and Stability of Heme Protein Induced by Imidazolium-Based Ionic Liquids. J Phys Chem B 119: 8357-8368.
- Bisht M, Kumar A, Venkatesu P (2015) Analysis of the Driving Force that Rule the Stability of Lysozyme in Alkylammonium-Based Ionic Liquids. Int J Biol Macromol 81: 1074-1081.
- Bisht M, Kumar A, Venkatesu P (2016) Refolding Effects of Partially Immiscible Ammonium-Based Ionic Liquids on the Urea-Induced Unfolded Lysozyme Structure Phys Chem Chem Phys 18: 12419-12422.
- Docherty KM, Kulpa JCF (2005) Toxicity and Antimicrobial Activity of Imidazolium and Pyridinium Ionic Liquids. Green Chem 7: 185-189.
- Cojocaru OA, Shamshina JL, Gurau G, Syguda A, Praczyk T, et al. (2013)Ionic Liquid Forms of the Herbicide Dicamba with Increased Efficacy and Reduced Volatility. Green Chem 15: 2110-2120.
- Goldfeder M, Fishman A (2014) Modulating Enzyme Activity Using Ionic Liquids or Surfactants. Appl. Microbiol. Biotechnol 98: 545-554.
- Zhao H (2016) Protein Stabilization and Enzyme Activation in Ionic Liquids: Specific Ion Effects. J. Chem. Technol. Biotechnol 91: 25-50.
- Yang Z (2009) Hofmeister Effects: An Explanation for the Impact of Ionic Liquids on Biocatalysis. J. Biotechnol. 144: 12-22.
- Zhao H, Olubajo O, Song Z, Sims AL, Person TE, et al. (2006) Effect of Kosmotropicity of Ionic Liquids on the Enzyme Stability in Aqueous Solutions. Bioorg Chem 34: 15-25.
- Zhao H (2006) Are Ionic Liquids Kosmotropic or Chaotropic? An Evaluation of Available Thermodynamic Parameters for Quantifying the Ion Kosmotropicity of Ionic Liquids. J Chem Technol Biotechnol 81: 877-891.
- Lai JQ, Li Z, Lu YH, Yang Z (2011) Specific Ion Effects of Ionic Liquids on Enzyme Activity and Stability. Green Chem 13: 1860-1868.
- Gao WW, Zhang FX, Zhang GX, Zhou CH (2015) Key factors affecting the activity and stability of enzymes in ionic liquids and novel applications in biocatalysis Biochem Eng J 99: 67-84.
- Naushad M, Alothman ZA, Khan AB, Ali M (2012) Effect of Ionic Liquid on Activity, Stability, and Structure of Enzymes: A Review. Int J Biol Macromol 51: 555-560.
- Zhao H (2005) Effect of Ions and Other Compatible Solutes on Enzyme Activity, and its Implication for Biocatalysis Using Ionic Liquids. J Mol Catal B: Enzym 37: 16-25.
- Weibels S, Syguda A, Herrmann C, Weingartner H (2012) Steering the Enzymatic Activity of Proteins by Ionic Liquids. A Case Study of the Enzyme Kinetics of Yeast Alcohol Dehydrogenase. Phys Chem Chem Phys 14: 4635-4639.
- Parsons DF, Bostrom M, Nostro PL, Ninham BW (2011) Hofmeister Effects: Interplay of Hydration, Nonelectrostatic Potentials, and Ion Size. Phys Chem Chem Phys 13: 12352-12367.
- Nelson DL, Lehninger AL, W. H. Freeman, Cox MM (2008) Lehninger Principles of Biochemistry.
- Heitz MP, Rupp JW (2017) Determining Mushroom Tyrosinase Inhibition by Imidazolium Ionic Liquids: A Spectroscopic and Molecular Docking Study. Int J Biol Macromol 107(B): 1971-1981.
- Constantinescu D, Weingartner H, Herrmann C (2007) Protein Denaturation by Ionic Liquids and the Hofmeister Series: A Case Study of Aqueous Solutions of Ribonuclease A. Angew Chem Int Ed Engl 46: 8887-8889.
- Yang Z, Yue YJ, Huang WC, Zhuang XM, Chen ZT et al. (2009) Importance of the Ionic Nature of Ionic Liquids in Affecting Enzyme Performance. J Biochem 145: 355-364.
- Yang Z, Yue YJ, Xing M (2008) Tyrosinase Activity in Ionic Liquids. Biotechnol Lett 30: 153-158.
- Goldfeder M, Egozy M, Ben-Yosef VS, Adir N, Fishman A, et al. (2013) Changes in Tyrosinase Specificity by Ionic Liquids and Sodium Dodecyl Sulfate. Appl Microbiol Biotechnol 97: 1953-1961.
- Espin JC, Wichers HJ (1999) Slow-Binding Inhibition of Mushroom (Agaricus bisporus) Tyrosinase Isoforms by Tropolone. J Agric Food Chem 47: 2638-2644.
- Grossfield A, Ren P, Ponder JW (2003) Ion Solvation Thermodynamics from Simulation with a Polarizable Force Field. J Am Chem Soc 125: 15671-15682.
- Spartan 16 (2016) Wavefunction Inc, 18401 Von Karman Avenue, Suite 370, Irvine, CA 92612, USA.
- Shao Y, Gan Z, Epifanovsky E, Gilbert ATB, Wormit M, et al. (2015) Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol Phys 113: 184-215.
- Marenich AV, Olson RM, Kelly CP, Cramer CJ, Truhlar DG et al. (2007) Self-Consistent Reaction Field Model for Aqueous and Nonaqueous Solutions Based on Accurate Polarized Partial Charges. J Chem Theory Comput 3: 2011-2033.
- Cornellas A, Perez L, Comelles F, Ribosa I, Manresa A, et al. (2011) Self-aggregation and antimicrobial activity of imidazolium and pyridinium based ionic liquids in aqueous solution. J Colloid Int Sci 355: 164-171.
- Lu L, Hu Y, Huang X, Qu Y (2012) A Bioelectrochemical Method for the Quantitative Description of the Hofmeister Effect of Ionic Liquids in Aqueous Solution. J Phys Chem B 116: 11075-11080.
- Constatinescu D, Herrmann C, Weingartner H (2010) Patterns of Protein Unfolding and Protein Aggregation in Ionic Liquids. Phys Chem Chem Phys 12: 1756-1763.
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences