Keywords

Trajectories; Neurodegeneration; Endophenotypes; Neuroimaging

Introduction

Bayesian approaches for imaging genetics have been developed to accommodate prior information on the relationship between neuroimaging endophenotypes and genetic variants while allowing for flexible modelling structures. These include joint probabilistic frameworks for imaging, genetic and disease data [1,2] and hierarchical models for relating neuroimaging and genetic data while accounting for spatial dependence [3,4]. The Bayesian framework allows naturally for the characterization of posterior uncertainty and inference which is an advantage over sparsity-based methods that emphasize point estimation. A substantial challenge associated with Bayesian methods within the context of imaging genetics however is the computation required for posterior approximation over a parameter space of high dimension. A Bayesian reduced rank model for relating imaging data to genetic markers that enables characterization of uncertainty for the regression parameters based on the posterior distribution while reducing the dimension of the regression coefficient matrix with a low rank approximation is developed in [5]. The model also incorporates a sparse latent factor structure for the covariance matrix of the neuroimaging data with a multiplicative gamma process prior assigned to the factor loadings. This low rank model is extended [6] to accommodate longitudinal imaging data through a random effects model where the regression structure allows for gene-age interactions so that the genetic effects on Region of Interest (ROI) volumes can vary across time [6] the author focus on longitudinal neuroimaging trajectories from a single region of interest obtained for a collection of subjects and use basis functions to model longitudinal trajectories of Magnetic Resonance Imaging (MRI) derived cortical volumes in neurodegeneration. The coefficients of the basis for individual subjects are assigned multivariate Gaussian priors with a covariance matrix that is based on biomarker kernels that allow for information sharing across subjects leading to a multi-task framework. The biomarker kernels allow for coupling of the trajectories across subjects based on APOE genotype, cerebrospinal fluid and amyloid Positron Emission Tomography (PET) based biomarkers. Develop a Bayesian multivariate linear model for relating an imaging response to genetic markers extending the group sparse multi-task regression and feature selection estimator developed by [7], to a setting allowing for fully Bayesian inference. The regression model is E(yl)=WT xl, l=1, . . . , n, where yl where yl is the c-dimensional imaging response and xl is a d-dimensional vector of genetic markers for subject l. Following the ideas of Park and Casell [8] develop a hierarchical model with a nested group lasso prior, where the grouping structure is at both the SNP and gene levels.

Imaging Genetics Studies

Letting W^(k) =(w_ij) denote the m_k ×c submatrix of W containing the rows corresponding to the kth gene, k = 1, . . . , K, and where mk is the number of SNPs included from gene k. The hierarchical model takes the form

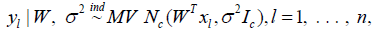
with the coefficients corresponding to different genes assumed conditionally independent 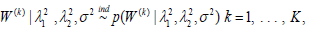and with the prior distribution for each W(k) having a density function that is based on a product of multivariate Laplace kernels

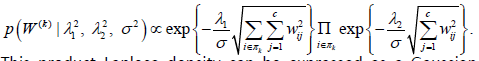
This product Laplace density can be expressed as a Gaussian scale mixture which allows for the implementation of Bayesian inference using a standard Gibbs sampling algorithm. The algorithm is implemented in the R package bgs mtr which is available for download on the Comprehensive R Archive Network (CRAN). In [9] the regression modelling framework is extended to allow for a more flexible covariance structure for modelling neuroimaging data by allowing for two forms of correlation seen in structural brain imaging data.

First, the model allows for spatial correlation in the imaging endophenotypes obtained from neighbouring regions of the brain or more generally on a graph linking the imaging endophenotypes on the same brain hemisphere. Second, the model allows for bilateral correlation between corresponding measures on opposite hemispheres of the brain. This joint spatial structure is based on a Bivariate Conditional Autoregressive Model (BCAR) [10]. The model relating the imaging and genetic data at the first level then takes the form

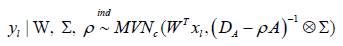
where A is a neighbourhood matrix imparting within-hemisphere spatial structure across regions, Ai is the ith row sum of A, DA=diag {Ai., i=1, ..., c/2}, ρ is a spatial dependence parameter, and Σ is a 2-by-2 matrix accounting for bilateral correlation across the brain. The prior for W is similar to the Gaussian scale mixture considered in [7] and formulated to encourage shrinkage at the SNP level across all neuroimaging endophenotypes. The prior additionally incorporates a bivariate structure for the regression coefficients corresponding to bilateral pairs of neuroimaging endophenotypes and their association with a given SNP. The spatial model is implemented using both a mean-field variational Bayes approximation to the posterior distribution as well as Markov Chain Monte Carlo (MCMC) sampling. The variational Bayes approximation is obtained by maximizing the evidence lower bound using coordinate ascent and is relatively fast and can be used to obtain an initial glance at the data as well as to initialize the MCMC sampler. Posterior samples are then used in conjunction with Bayesian FDR for SNP selection, [11] develop a novel regression approach based on a semiparametric conditional graphical model for imaging genetics that is developed to infer genetic associations on multivariate neuroimaging endophenotypes while simultaneously inferring functional brain connectivity [11]. Prior distributions on the regression coefficients in the multivariate regression are based on a generalization of a Dirichlet process mixture of Laplace distributions which facilitates clustering of the regression coefficient vectors corresponding to individual imaging outcomes into groups. Each individual group is treated as a module in a functional modular network. Conditional on the clustering defining the modules the covariance matrix is assigned a semiParametric hyper inverse-Wishart prior defined over a graph with edge structure depending on the clustering and hyperpriors chosen so that the resulting graph has a higher density of edges within modules and a lower density of edges connecting modules. An MCMC algorithm is developed to infer the brain network and genetic associations simultaneously [12]. Develop a regression approach that is amenable to handling voxel-specific imaging endophenotypes. The approach is based on partitioning the brain into regions of interest and treating the imaging response obtained at all voxels within each ROI independently. Thus a separate multivariate regression model relating imaging measures collected over voxels onto genetic variants is considered at each ROI and the approach is applied to all ROIs in parallel. At each ROI generalized principal component analysis is used to project the response to a lower dimension and the projected response is then related to genetic variants using a linear model combined with Bayesian model averaging to account for the collection of models that arise from inclusion/exclusion of each individual covariate. A uniform prior is placed over the model space and a g-prior is assigned to the vector of regression coefficients conditional on the model sample from the posterior distribution over the model space and regression coefficients, characterizing the relationship between the projected imaging response and genetic variants using MCMC. The authors then use a reverse projection to map the sampled regression parameters defined over the dimension-reduced space obtained from GPCA to the original space of voxels within ROIs.

Discussion

As an alternative to regression modelling relating preselected neuroimaging endophenotypes to genetic variants [12] develop a Bayesian probabilistic framework for jointly modelling disease, neuroimaging and genetic data. The joint modelling of imaging, genetics and disease is a novel aspect of this Bayesian approach. The approach is based on a joint model with two primary regression specifications, the first being a logistic regression relating a binary disease response to image features and the second relating the imaging features to the genetic variants. The logistic regression is then extended to a more flexible Gaussian process logistic regression. A key aspect of the hierarchical framework is the use of spike-and-slab priors at two nested levels which serve to stochastically couple the disease-imaging and imaging-genetic regression models. At the first level, latent selection variables in the logistic regression encode which components of the imaging feature are related to disease while at a second level, selection variables encode which genetic variants are related to specific imaging features, conditional on the selection variables at the first level indicating that a specific feature is related to disease.

Conclusion

While the development of Bayesian methods for imaging genetics has seen steady development there is tremendous scope for further work. A pressing issue is the development of computational methods for implementing Bayesian methods that are able to scale in this context while maintaining a reasonable degree of accuracy. The potential of divide and conquer sampling approaches such as the likelihood inflated sampling algorithm and further investigation of variational methods and the combining of variational methods with stochastic approximations may be promising avenues of investigation. In addition, further development of semiparametric Bayesian methods along the lines investigated by are also important lines of further development.

Inference on these latent variables can reveal how different components of the imaging endophenotypes relevant to disease are related to each of the genetic variants, thus revealing the spatial distribution. With spike-and-slab priors nested at two levels in high-dimensions the implementation of Bayesian inference is challenging and the authors combine variational Bayes with stochastic approximations to simultaneously infer on the genetic variants and imaging features associated with disease. The ability to conduct simultaneous inference considering disease, imaging and genetics jointly is an important advantage of this approach.

Acknowledgement

Research is supported by funding from the Natural Sciences and Engineering Research Council of Canada and the Canadian Statistical Sciences Institute. F.S. Nathoo holds a Tier II Canada Research Chair in Biostatistics for Spatial and High-Dimensional Data.

References

1. Batmanghelich NK, Dalca A, Quon G, Sabuncu M, Golland P (2016) Probabilistic modeling of imaging, genetics and diagnosis. IEEE Trans Med Imaging 35: 1765-79.
2. Batmanghelich NK, Dalca A, Sabuncu MR, Polina G, ADNI (2013) Joint modeling of imaging and genetics. Inf Process Med Imaging 23: 766-77.
3. Song Y, Ge S, Cao J, Wang L, Nathoo FS (2021) A Bayesian spatial model for imaging genetics. Biometrics 22: 701-714.
4. Stingo FC, Guindani M, Vannucci M, Calhoun VD (2013) An Integrative Bayesian Modeling Approach to Imaging Genetics. J Am Stat Assoc 108: 876â??891.
5. Zhu H, Khondker Z, Lu Z, Ibrahim JG, (2014) Bayesian Generalized Low Rank Regression Models for Neuroimaging Phenotypes and Genetic Markers. J Am Stat Assoc 109: 997-990.
6. Aksman LM, Scelsi MA, Marquand AF, Alexander DC, Ourselin S, et al. (2019) Modeling longitudinal imaging biomarkers with parametric Bayesian multi-task learning. Hum Brain Mapp 40: 3982â??4000.
7. Greenlaw K, Szefer E, Graham J, Lesperance M, Nathoo FS, et al. (2017) A Bayesian group sparse multi-task regression model for imaging genetics. Bioinformatics 33: 2513-2522.
8. Wang H, Nie F, Huang H, Kim S, Nho K, et al. (2012) Identifying quantitative trait loci via group-sparse multitask regression and feature selection: An imaging genetics study of the ADNI cohort. Bioinformatics 28: 229-37.
9. Casella G, Ghosh M, Gill J, Kyung M (2010) Penalized regression, standard errors, and Bayesian lassos. Bayesian Analysis 5: 369-411.
10.  AE, Vounatsou P (2003) Proper multivariate conditional autoregressive models for spatial data anal Gelfand ysis. Biostatistics 4: 11-25.
11. Kundu S, Kang J (2016) Semiparametric Bayes conditional graphical models for imaging genetics applications. Stat (Int Stat Inst) 5: 322-337.
12. Azadeh S, Hobbs BP, Ma L, Nielsen DA, Moeller FG, et al. (2016) Integrative Bayesian analysis of neuroimaging-genetic data through hierarchical dimension reduction.  Proc IEEE Int Symp Biomed Imaging 824-828.