Keywords

Darcy’s extended law; Anisotropy; Sedimentary; Fractal and Nonequilibrium

Nomenclature

α: Aspect ratio,

d: Dimension,

G: Conductance matrix,

H: Hurst exponent,

J: Thermodynamic flux,

K₁₂: Capillary transport coefficient of non-wetting phase,

K₂₂: Capillary transport coefficient of wetting phase,

K₁₁: Effective permeability of non-wetting phase,

K₂₁: Effective permeability of wetting phase,

l: Cutoff length,

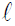: Length,

L: Phenomenological coefficient,

P: Pressure,

P_c: Capillary pressure,

Q: Average flow rate,

r: The radius of the throat,

R: The radius of the pore or throat,

X: Driving force,

S: Power spectrum,

ω: Frequency,

η: Anisotropy parameter.

Subscripts

co: Cutoff,

j: The numbers of the driving forces,

nw: Non-wetting,

p: Pore,

t: Throat,

w: Wetting.

Introduction

Darcy’s law has been extended by the concepts of the effective and relative permeabilities in two-phase flow for the situation in which the ability of each fluid to flow is reduced by the presence of other fluid. Using the average of the Navier-Stokes equation for a fluid that occupies only part of the void space, Bear [1] indicated that the effective permeabilities of anisotropic porous medium are also symmetric second rank tensors. The rank of a tensor is defined by the number of directions required to describe it. The physical properties that require two directions to be described are second rank tensors. Up to now, the effective permeabilities of anisotropic porous medium require two directions to be described in the anisotropic porous media. One is the direction of the macroscopic pressure gradient and other is the principal directions of anisotropic porous media. The Navier- Stokes equation does not include terms which characterize interactions between the fluids and the surface of the solid or the capillary forces. Therefore, Darcy’ extended law based on Navierstokes equation can’t consist of the capillary force term in the macroscopic scale. If we consider interactions between the fluids and the surface of the solid or the capillary forces in the average equation of motion in laminar flow through an anisotropic porous medium in macroscopic capillary non-equilibrium situation, the effective permeabilities of the anisotropic porous medium may require three directions to be described under this situation. If we need to consider three directions to describe a physical property, the physical property is a third rank tensor. As if, the rank of the effective permeability tensor may be greater than second rank tensor in the capillary non-equilibrium situations through an anisotropic porous media. If the rank of the effective permeability tensor is greater than second rank tensor, Darcy’s law cannot be extended to an anisotropic porous media in the capillary non-equilibrium situations. The transport coefficient in Darcy’s extended law, effective permeability, between the flow and pressure gradient vectors which have two elements in a twodimensional and three elements in a three-dimensional can be expressed as a scalar quantity or a second rank tensor and cannot be expressed as a third rank tensor.

Another concept describing two-phase flow in porous media and used in Darcy’s extended law is scalar relative permeability. In scalar relative permeability theory, the ability of the one fluid to flow is reduced by the presence of the flow of other fluid through porous media. The flow of each phase is inhibited by the presence of the other phase in the absence of interaction between fluids and the capillary forces. Thus, the sum of relative permeabilities of two phases is almost equal to or less than one.

At first, Darcy’s extended law had been formulated for immiscible multiphase flow in isotropic porous media. Then, it was used for anisotropic porous media. Bear et al. [2] expressed that the concept of relative permeability used in two phase flow should be limited to isotropic media and no extended to anisotropic ones.

In Darcy’s extended law, it is assumed that interactions between the fluid-fluid and between the fluid and the surface of the solid are neglected. Under this assumption, the relative permeability depends only on the saturation and relative permeability is supposed as a scalar quantity in anisotropic reservoir simulation. This assumption is not valid since interactions between the fluids and the surface of the solid in capillary non-equilibrium situation and the interactions between two fluids in steady-state concurrent twophase flow are important in anisotropic porous media.

Can Darcy’s extended law be used through the sedimentary medium for the capillary non-equilibrium situations? This study answers to this important questions. At first, we are to investigate the effect of the capillary force on relative permeability. Then, we are to investigate the ability of the Darcy’s law to be extended in two-phase flow for the sedimentary medium in the capillary nonequilibrium situations. We are not to study the viscous coupling effect derived from the interactions between the wetting and nonwetting fluids that can flow simultaneously in a pore on relative permeability in steady-state concurrent adjacent flow of two immiscible fluids through porous media. We neglect the wetting phase film flow in corners. Relative permeability as a function of saturation may depend on the direction of the capillary force. The performed investigations on relative permeability anisotropy are very scarce and limit.

Corey and Rathjens [3] showed the dependence of relative permeability on flow orientation in the presence of laminated bedding in a core and proposed that the dependence was related to capillary difference caused by grains-size differences. Kortekaas [4] used a reservoir simulator to show the effects of relative permeability anisotropy through cross-bedding in sandstones. Bear et al. [2] used a model composed of a three-dimensional orthogonal network of capillary tubes to simulate the flow behavior in an unsaturated anisotropic soil. They concluded that the components of relative permeability anisotropy tensor do not constitute components of a second rank tensor and there seen to be no advantage in extending the definition and concept of relative permeability to anisotropic porous media. Inversion et al. [5] measured relative permeability on Tensleep sandstone samples from Wyoming using unsteady state technique, described by Ajdari [6], and their measurements demonstrated the magnitude and character of relative permeability anisotropy. They showed that the relative permeability measured in the parallel direction is slightly greater than that measured in the vertical direction to the bedding. Paterson et al. [7] investigated the effect of statistical heterogeneity on relative permeability and residual saturation using network model simulations. They interpreted site occupancy in terms of porosity available to each fluid and related throat radii to permeability. They concluded that relative permeability is sensitive to the degree of correlation and anisotropy in pore scale properties and relative permeability is greater for flow parallel to the bedding composed with flow perpendicular to the bedding.

The purpose of this study is to investigate the ability of Darcy’s law for extending in two-phase flow for the sedimentary medium in the capillary non-equilibrium situations in order to calculate accurately wetting and non-wetting fluid flow rates. If relative and effective permeabilities depend on the direction of the capillary force and relative permeability cannot be expressed as scalar quantity or a second rank tensor, Darcy’s law cannot be extended to the sedimentary medium in the capillary nonequilibrium situations. We are to offer a new relationship to calculate accurately wetting and non-wetting flow rates through the sedimentary medium in the capillary non-equilibrium situations. In this study, anisotropy of relative permeability is investigated using pore network modeling and demonstrated by comparing relative permeabilities in the principal directions of anisotropy. The traditional anisotropy used in previous network models was the type in which the sizes of the pores and throats in each direction were distributed according to a distinct probability distribution function. This anisotropy type used in pore network modeling for the macroscopic properties such as the hydraulic resistances in the principal directions generated by different probability distribution functions for the radii of the pores and throats in each of the principal directions is mostly similar to isotropic model in macroscopic scale. We are to investigate the anisotropy that is caused by layering which is what happens in natural sedimentary medium. At first, we have simulated the sedimentary medium as the correlated anisotropic network model. Then, the capillary non-equilibrium situation has been demonstrated in two-phase flow through the sedimentary medium. At last, we have generated the pore network model in which the sedimentary medium and the capillary non-equilibrium situation have been simulated and relative permeability is calculated in each direction.

Sedimentary Medium and Correlated Heterogeneity

If a physical property of the medium varies with direction at a point within the medium, the medium is said to be anisotropic at the considered point with respect to that property. In sedimentary medium, the hydraulic conductance of the flow for parallel direction to the bedding is greater than that for perpendicular direction to the bedding. If a certain property of a medium depends on position within the medium, the medium is said to be heterogeneity with respect to that property. Sedimentation and pressure of overlying material cause to increase permeability, connection between void spaces and correlation between the narrower regions of the void spaces in parallel direction to the layers.

The heterogeneity exists at pores, core plugs and field length scales in the reservoir. Hewett [8] proposed that the porosity logs and permeability distribution of field-scale porous media follow fractal statistics. He concluded that the porosity logs in the perpendicular direction to the bedding may obey the statistics of fractional Gaussian noise, while those parallel to the bedding follow a fractional Brownian motion. The percolation model of flow in porous media in which the long-range correlations were generated by a fractional Brownian motion was first proposed by Sahimi [9]. The motivation for his model was provided by the work of Hewett [8]. In previous pore network models to modeling of multiphase flow in porous media, correlations in the pore and throat size distribution have been neglect. Long-range correlation exists at the pore [10,11] and field scales in sedimentary medium. There are very limited studies of the effect of correlations in the pore and throat size distribution on the important characteristics such as capillary pressure [11] and relative permeability of sedimentary rocks. There are distinct long-rang correlations for the radii of the throats in each of the parallel and perpendicular directions to the bedding in the sedimentary medium. We have suggested that the throat size distribution can be described by fractional Brownian motion.

If there are long-rang correlations described by fractional Brownian motion for the radii of the throats, the variance is given by:

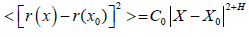   (1)

Where C0 is a constant, and X and X0 are two points in the throat space. The Hurst exponent H determines the nature of the correlations. The Hurst exponent is related to the fractal dimension and the Hurst exponent range from 0 to 1, taking the value H=0.5, H>0.5, and H<0.5, respectively for uncorrelated, correlated and anti-correlated Brownian motion. The type and extend of the correlations can be tuned by varying the Hurst exponent.

The power spectrum S(ω) of a d-dimensional fractional Brownian motion is given by:

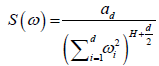   (2)

Where ω=( ω1, …, ω d) and αi is a constant. Many fractal systems lose their fractality above a cutoff length scale. The spectral representation of a stochastic process allows a convenient way of introducing this cutoff length scale. Thus, we introduce the cutoff length scale 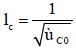such that

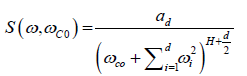   (3)

By tuning the cutoff length scale one can control the length scale over which the spatial properties of a system are correlated (or anti correlated). Hence, for length scales l< lC0 they preserve their correlations (anti correlations), but for l> lC0 they become random and uncorrelated. The introduction of the cutoff length scale allows us to choose an appropriate length scale for correlations at the pore scale. We generate the anisotropy and the correlation for a two-dimensional fractional Brownian motion as following:

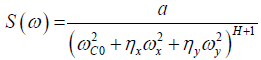   (4)

Where η_x and η_y are the anisotropy parameters and are constant. The anisotropy is generated by varying anisotropy parameters η_x and η_y. The type of the anisotropy can be tuned by varying anisotropy parameters η_x and η_y. The layers are generated by varying anisotropy parameters. When anisotropy parameters in Y and X directions are equal to and less than one, respectively, the generated layers are essentially parallel to the X direction and vice versa.

We have used a fractional Brownian motion characterized by the cutoff lengths and anisotropy parameters in the parallel and perpendicular directions to the bedding and a Hurst exponent to generate a correlated anisotropic network model to represent the sedimentary medium. We have employed the correlated pore network modeling with trapping with long-rang correlation to model slow flow of fluid in the sedimentary medium. We have generated a two-dimensional fractional Brownian motion array using equation (4) and have assigned the resulting numbers to the throat of the two-dimensional lattice. The numbers generated by fractional Brownian motion are then taken as the radii of the throats.

We have generated the correlated anisotropic network model by a fractional Brownian motion characterized by a cutoff length lC, anisotropy parameters η_x and η_y, and a Hurst exponent H to represent the sedimentary medium. Then, we have generated the correlated anisotropy network model by a two-dimensional multi fractal Brownian motion characterized by a Hurst exponent that is as a function. Then, the multi-fractal Brownian motion is generated from the FracLab software [12] developed by INRIA. It is supposed that there are the most correlations in the central of the layers in the parallel direction to them and the least correlations in the interface of the layers in the perpendicular direction to them. In this method, the Hurst exponent is a function as following:

   (5)

We applied the fractal distributions to the radii of the throats. The random pore network modeling is a representation of the very small section of the reservoir rocks. But, this network models generated by the fractional and multi-fractional Brownian motions are the representation of the sedimentary rocks and contains information from different length-scales (multi scale network).

Capillary Pressure

The traditional definition of the macroscopic capillary pressure is as the pressure difference between the non-wetting and wetting phase in capillary equilibrium situations. This definition is correct when the non-wetting and wetting macroscopic and microscopic interfaces is constant and the system is under capillary equilibrium situation. The macroscopic definition of the capillary pressure is derived from the microscopic definition of the capillary pressure. The traditional capillary pressure is expressed as a scalar quantity and as a function of the wetting phase saturation and is independent of direction. Bear [1] defined that the capillary pressure is a measure of the tendency of a porous medium to suck in the wetting phase or to repel the nonwetting phase. Other definition of capillary pressure in porous media used in laboratory measurements is the necessary force or pressure difference to displace the wetting phase by the nonwetting phase. Hassanizadeh and Gray [13] reported that the capillary pressure as a function of the difference in the average pressure of non-wetting and wetting phases, must viewed as an equilibrium force balance and not as a definition of capillary pressure. They proposed that capillary pressure is related to the change in free energy.

Hassanizadeh et al. [14] expressed that there are two types of capillary pressure. The first is static capillary pressure which is defined as the pressure difference between non-wetting and wetting phases in equilibrium situation. The static capillary pressure depends on saturation. The second is the dynamic capillary pressure which is defined as the pressure difference between non-wetting and wetting phases in non-equilibrium situation. The dynamic capillary pressure depends on the saturation and the fluid-fluid interface area. Joekar-Niasar et al. [15] proposed the definition of the macroscopic capillary pressure based on the average of local capillary pressure at all interfaces weighted with the area of the interface.

There are two different types of interfaces in pore network. The first is the microscopic interface which is interfaces in corners and edges. The second is macroscopic interface which is interfaces between invaded pores and their connecting throats which have not yet been invaded. We have considered the macroscopic interface that is interfaces between invaded pores and their connecting throats which have not yet been invaded in macroscopic scale.

Brooks and Corey [16] found the relationship between the capillary pressure and the pore size distribution index and the normalized wetting phase saturation. They related the pore size distribution index to the distribution of pore size. Li [17] related the pore size distribution index to the fractal dimension of the porous media. The magnitude of fractal dimension is a representation of the heterogeneity of the porous media. The pore size distribution index in the Brooks-Corey model is a representation of the heterogeneity of porous media. In sedimentary medium, the pore throat size distribution and the fractal dimension in the parallel direction to the bedding are different from those in the perpendicular direction to the bedding. Thus, for capillary nonequilibrium situation in the sedimentary medium, the capillary pressures in the principal directions are different. Joekar-Niasar et al. [15] expressed that the capillary pressure-saturation relationship is not unique and, even though it is obtained under equilibrium condition, it is a function of the history of fluids movements and it depends not only on the volume fraction of each phase but also on their micro-scale distribution.

In imbibition process, the wetting fluid displaces the non-wetting fluid by capillary forces without applied pressure gradient. The capillary pressure is created by the wetting phase saturation gradient throughout porous media. The capillary forces are as driving force in an anisotropic porous media in the capillary nonequilibrium situations. The capillary forces in drainage process are as resisting forces for non-wetting and wetting fluid flow rate. The capillary forces in imbibition process are as assisting forces for wetting and non-wetting fluid flow rate. Thus, the capillary force in two-phase flow can acts as the conductance or resistance of the sedimentary medium. Hassanizadeh and Gray [13] derived the extended form of Darcy’s law in which gradients of saturation and specific interfacial area appeared as driving forces. The changes of the saturation and specific interfacial area in capillary non-equilibrium situation are the representation of the capillary driving force. For capillary non-equilibrium and dynamic situation, the capillary forces are as a potential gradient throughout the principal directions and these capillary forces are not constant in the principal directions. When the macroscopic pressure difference is applied between inlet and outlet faces in network model, there are two driving forces. The first is the applied pressure difference and the second is macroscopic capillary pressure or force.

As the local capillary pressures with the different interface areas and the different local wetting phase saturations in inlet and outlet faces are considered in drainage process, the local capillary pressure of the inlet face is greater than the local capillary pressure of the outlet face. Since, the wetting phase saturation of the inlet face is less than that of the outlet face. The area of the interface of the inlet face is more than that of the outlet face before the breakthrough.

We assume two capillary pressures in pore network modeling. The first is the microscopic or threshold capillary pressure which depends on the radius of the throat. The second is the macroscopic capillary pressures which are different in the principal directions through an anisotropic network. The macroscopic capillary pressures are induced by capillary force which enforces on the system to reach capillary equilibrium in the principal directions. We simulate the macroscopic capillary pressures in drainage process as the tendency of the non-wetting fluid to invade the largest throat connected to non-wetting phase in a displacement. The drainage process is simulated as a consecutive sequence of displacements of non-wetting phase in the larger throats. The capillary non-equilibrium situation is simulated by the competition between the larger throats connected to non-wetting phase in the principal directions to be invaded by non-wetting phase for drainage process, even though pressure gradient vector is in another direction. The macroscopic capillary pressures in principal directions are different in an anisotropic porous media in macroscopic capillary nonequilibrium situation. Therefore, when the imposed macroscopic pressure difference is in one direction, the components of nonwetting and wetting fluid flows due to the macroscopic capillary pressures in the principal directions of the anisotropic porous media in macroscopic capillary non-equilibrium situation are in other directions.

Network Modeling

Pore network modeling has been used to predict transport flow macroscopic properties such as capillary pressure and relative permeability for two-phase flow. The porous medium is represented by the network modeling which was pioneered by Fatt [18]. The pore network model represents the void space of the porous media by a regular cubic or square lattice of wide pores connected by narrower regions called throats. The throats represent the main resistance to the flow. The fluid flow is controlled by the radii of the throats in two-phase flow in porous media. We have used a sphere-and-tube model with pores and throats. Thus, it is assumed that the throats are cylinders with circular cross-sections and pores are spherical. In this case, they can only contain one fluid. We neglect the wetting phase film flow in corners. We have used the dynamic pore network model in which the viscous and capillary forces are modeled and the pressure field is calculated.

We modeled drainage process in which non-wetting fluid displaces wetting fluid, through an anisotropic network model in the capillary non-equilibrium situation. We have simulated the sequence of the displacements induced by imposed macroscopic pressure differences and created capillary forces in drainage process through the anisotropic network model in capillary nonequilibrium situation. There are two potential gradients in each displacement in drainage process throughout an anisotropic network in capillary non-equilibrium situation. One is the macroscopic pressure difference of the inflow and outflow faces and other is macroscopic capillary pressure difference.

Initially, the network is assumed to be completely filled with a wetting fluid. The constant pressure difference is applied at the inflow and outflow faces. The pressure in each pore is calculated by solving volumetric balance equation for every pore with an imposed constant pressure difference between the inlet and outlet faces. For drainage process simulation, the inlet face of the pore network is considered to be connected to a non-wetting phase. High and low faces are assumed to be no-flow boundaries. The non-wetting fluid is injected into the network from the inflow side with a constant pressure difference between the inflow and outflow faces. We have modeled competition between the viscous and macroscopic capillary forces in two-phase flow through the simulated sedimentary medium for the capillary non-equilibrium situations using the correlated anisotropic network model. Since, the relative permeability curve as a function of saturation depends on the paths of the non-wetting phase movement in drainage process in anisotropic porous media. The competition between the viscous and macroscopic capillary forces is simulated by competition between throats to be invaded by non-wetting phase in each displacement for drainage process. If the viscous force is simulated in network model for drainage process in each displacement, a throat will be invaded by non-wetting phase in which the pressure difference between the invaded and noninvaded pores connected to it minus the entry capillary pressure of it is the largest. If the capillary force in addition the viscous force are simulated in network model for drainage process in each displacement, a throat will be invaded by non-wetting phase which is the largest throat connected to non-wetting phase. The viscous and capillary forces are considered until the effective permeability requires three directions to be described in anisotropic porous media. If the pores connected to a noninvaded throat are invaded by non-wetting fluid, the wetting fluid is trapped in that throat. We separate the microscopic and macroscopic capillary pressure. It is assumed that there are two capillary pressures in this network model. The first is a threshold or entry capillary pressure which depends on the radius of the throat and interfacial tensions and contact angles. The second is the macroscopic capillary pressure which is created by capillary force in each of principal directions and determines the nonwetting phase movement paths. It is assumed that the pressure difference between non-wetting and wetting phases and the macroscopic configuration and area of the interface of the nonwetting and wetting fluids in macroscopic scale throughout porous media are induced by the macroscopic capillary pressure in capillary non-equilibrium situation. After injecting non-wetting fluid into the network and the breakthrough, the pressure in each pore is calculated by solving volumetric balance equations for pores. Then, the flow rates through network are calculated for non-wetting and wetting fluids. If a cluster of wetting phase disconnects to the outlet, it is trapped. If a throat or cluster of throats which is filled by the defending fluid is surrounded by the invading fluid, it is trapped.

In this study, it is assumed that the fluids are Newtonian, incompressible, and immiscible. It is assumed that the Reynolds and capillary numbers and the fluid velocity in throats are low enough such that the fluid flow is capillary controlled at the pore scale. We neglect the gravity force and the resistance of the pore and the wetting fluid flow in corners. It is assumed that the imposed pressure difference between the inflow and outflow faces is large enough on the network such that the network is in the capillary non-equilibrium situations. We have applied a large global pressure difference on the network.

We have used the correlated model to calculate the throat radii. We have used fractal model to assign the values of the radii of the throats. The radii of the pores should be greater to the maximum radius of the connecting throats. Therefore, the radii of the pores are given by the following expression:

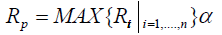   (6)

Where n is the number of the connecting throats and the aspect ratio α is the ratio between the pore radius and the maximum radius of the connecting throats. It is assumed that the maximum and minimum aspect ratios are equal to 2 and 2.2, respectively. The aspect ratios and throat radii are calculated as following.

We have used fractal distribution to assign the radii of the throats. It is assumed that there are distinct correlations for the radii of the throats in the parallel and perpendicular directions to the bedding which follow from fractal statistical. We have used the power spectrum of two-dimensional fractional Brownian motion characterized by the distinct cutoff lengths and anisotropy parameters in the parallel and perpendicular directions to the bedding and a Hurst exponent as equation (4) to calculate the radii of the throats and the aspect ratios in the parallel and perpendicular directions to the bedding. Then, we have used multi-fractal Brownian motion generated by FracLab software with the Hurst exponent function as equation (5) to calculate the radii of the throats and the aspect ratios in the parallel and perpendicular directions to the layers. The multi-fractal Brownian motion is a generalization of fractional Brownian motion where the Hurst exponent is allowed to vary along the path instead of remaining fixed.

In our model, the length of a throat is equal to the spacing of the lattice points minus the sum of radii of the two neighboring pores.

Drainage process is simulated by the applied macroscopic pressure gradient across the network and reaching to capillary equilibrium. Total flow rate for each fluid through the anisotropic network model in each direction in macroscopic scale is as following:

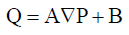   (7)

In this expression ∇P is the applied macroscopic pressure gradient across the network and B is the representation of the macroscopic capillary pressure gradient in each direction.

We have applied the constant pressure difference at the inlet and outlet faces of the network. The set of equations obtained from the conservation of volume at each pore is written as a matrix system:

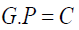   (8)

With G matrix of the conductance, P vector of unknown (pressure in each pore) and C vector of constants (capillary pressure, inlet and outlet pressures). If matrix G is symmetric, the solution of the system is obtained using a conjugate gradient method. As matrix G is not symmetric, the solution of the system is obtained using a bi-conjugate gradient method. The total flow rate of the only phase filling network can be calculated using the pore pressure obtained from the conservation of volume at each pore. The nonwetting and wetting fluid flow rates are calculated from the fluxes through boundary throats connected the inlet and outlet faces.

When the non-wetting and wetting phases span through the network from inlet to outlet, the relative permeability of the non wetting and wetting phases are calculated using the total flow rate and the wetting and non-wetting fluid flow rates obtained from the pressure of the pores.

The Thermodynamic Theory of Nonequilibrium Processes

The thermodynamics of irreversible processes is based on the linear law and the Onsager reciprocal relationship. There exist a large number of constitutive equations describing irreversible processes in form of linear relationship between fluxes and driving forces. The linear constitutive laws of irreversible thermodynamics postulate that the thermodynamic fluxes, Jk, are linearly proportional to the driving forces, Xj, as following:

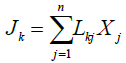    (9)

These equations are called phenomenological equations. The coefficients Lkj are called the phenomenological or transport coefficients which are characteristic of each system. The laws of Fourier, Fick and Newton express a linear relationship between a flux and its conjugated force. These relationships are accepted to be correct at the macroscopic scale.

In isotropic systems, the transport coefficients are as scalar. In anisotropic systems, when the driving force vector is in one direction, the components of the flow flux vector are in another direction. Therefore, transport coefficients cannot be expressed as scalar. The transport coefficients require two directions to be described. Therefore, they are second rank tensor. Darcy’s extension law is a linear relationship between the flow rate and the driving forces which are the gravity and the imposed macroscopic pressure gradient. We have used the thermodynamics theory of non-equilibrium process to calculate two-phase flow rate through anisotropic porous media for capillary non-equilibrium situation.

Results and Discussion

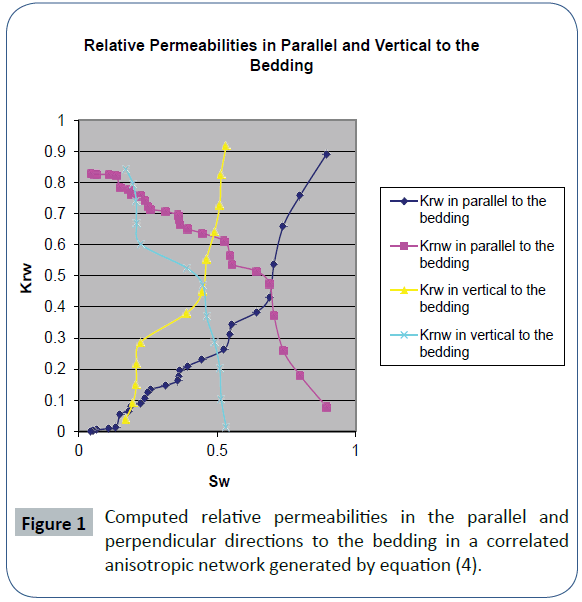
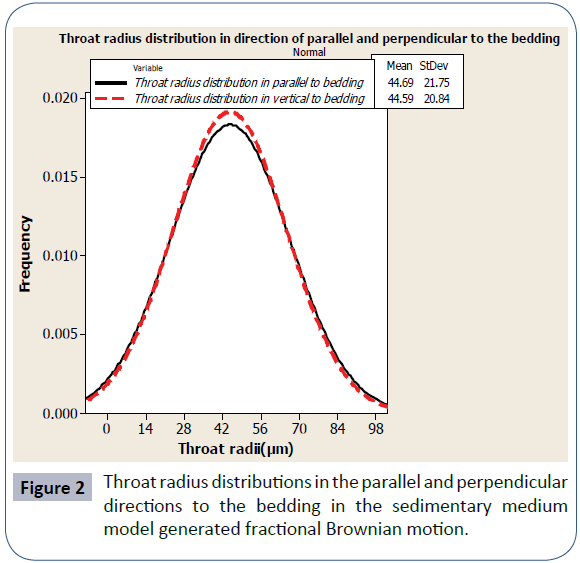
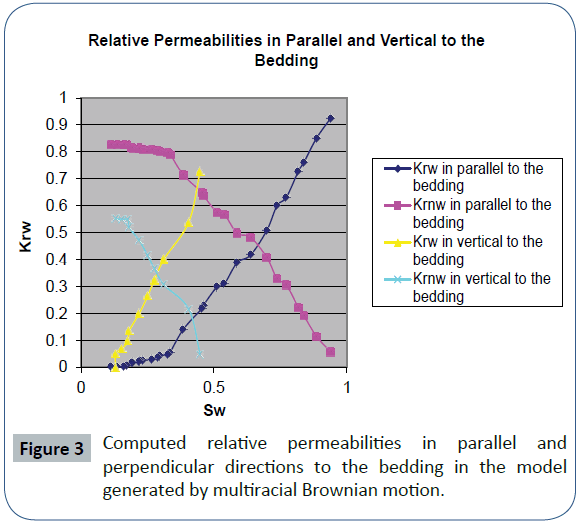
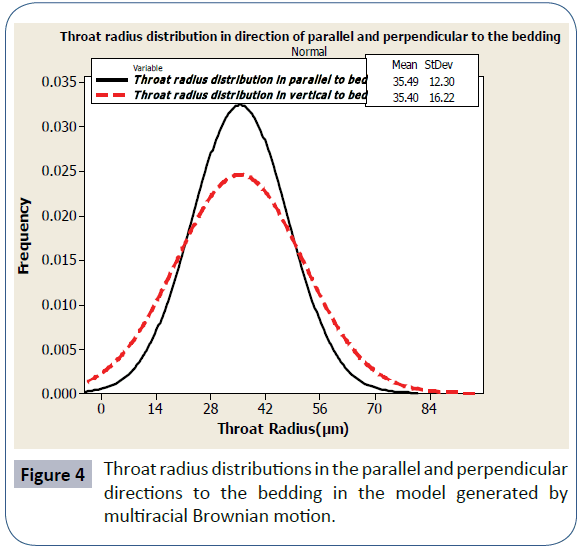
We have used the pore network modeling with trapping to investigate the dependence of the relative permeability on the direction for the sedimentary medium in the capillary nonequilibrium situations for drainage process. The sedimentary medium is represented as the anisotropic correlated network in which there are distinct correlations for the radii of the throats in the parallel and perpendicular directions to the bedding. There are the distinct correlations for the radii of the throats in the parallel and perpendicular directions to the bedding in the sedimentary medium. The anisotropic correlated network model has been formed from the sets of throats whose the radii are calculated with distinct cutoff lengths and anisotropy parameters in the parallel and perpendicular directions to the bedding. The number of the grids in each of the parallel and perpendicular directions to the bedding is 128. We have used a two-dimensional fractional Brownian motion characterized by the cutoff lengths in the principal directions (lcx and lcy), the anisotropy parameters for the principal directions (η_x and η_y) and a Hurst exponent H to generate the sedimentary medium. The sedimentary medium model is generated by taking values ∞ and 16 for the cutoff lengths in the parallel and perpendicular directions to the bedding respectively and values 0.01 and 1 for anisotropy parameters (η_x and η_y) in the parallel and perpendicular directions to the bedding respectively in equation (4). When lc=∞, the extent of the correlations is as large as the linear size of the network. Calculated relative permeabilities in the parallel and perpendicular directions to the bedding in anisotropic correlated network model generated by equation (4) are shown in Figure 1. The relative permeability curve as a function of saturation depends on the paths of non-wetting phase movement for drainage process in the sedimentary medium for the capillary non-equilibrium situations. The Figure 2 compares the radii of the throats with normal distribution in the two parallel and perpendicular directions to the bedding for the correlated anisotropic network generated by equation (4). In the sedimentary medium simulated as the anisotropic correlated network model, relative permeability for non-wetting phase in the parallel direction to the bedding is greater than that in the perpendicular direction to the bedding. The throat size distributions in two parallel and perpendicular directions to the bedding of the correlated anisotropic network are the same. The reason of this difference in relative permeability curves is the distinct correlations between the throat radii in the parallel and perpendicular directions to the bedding in the sedimentary medium. Relative permeability for non-wetting phase in the parallel direction to the bedding is greater than that in the perpendicular direction to the bedding because the correlation length in the parallel direction to the bedding is greater than that in the perpendicular direction to the bedding. Then, we have used a multi-fractional Brownian motion generated by FracLab software with the Hurst exponent function (5) to generate a correlated anisotropic network model. The visualization of this model generated by multi-fractional Brownian motion is almost the same as the previous model generated by fractional Brownian motion characterized by cutoff lengths, anisotropy parameters and a Hurst exponent. Calculated relative permeabilities in the parallel and perpendicular directions to the bedding in the anisotropic correlated network model generated by multifractional Brownian motion with the Hurst exponent function as equation (5) are shown in Figure 3. The Figure 4 compares the radii of the throats with normal distribution in the two parallel and perpendicular directions to the bedding for the anisotropic correlated network model generated by multi-fractional Brownian motion. The relative permeability of non-wetting phase in the parallel direction to the bedding is greater than that in the perpendicular direction to the bedding in network model simulated by multi-fractional Brownian motion. The reason of this difference is the distinct correlations for the radii of the throats, controlling fluid flow, in the parallel and perpendicular directions to the bedding in the sedimentary medium. When the larger throats of the network lie in one direction, non-wetting fluid flows in that direction in drainage process although pressure gradient vector is in another direction. The non-wetting and wetting fluid tend to flow in directions or through paths to reach the capillary equilibrium, even when they are forced by pressure gradient to flow in another direction.

Relative permeability depends on direction of the capillary force in the sedimentary medium. Up to now, it is assumed that relative permeability is expressed as a scalar quantity and the effective permeability of the sedimentary medium requires two directions to be described. But, we have shown that the effective permeability of the sedimentary medium in the capillary nonequilibrium situations requires three directions to be described. The new dimension of the effective permeability is the capillary driving force. If the rank of the effective permeability is larger than the second rank tensor, the Darcy’s law cannot be extended to anisotropic porous media in capillary non-equilibrium situation. We have offered new relationship to calculate twophase flow rate through anisotropic porous media in the capillary non-equilibrium situations.

We consider the local capillary pressures in the inflow and outflow faces of the network based on the local saturations in the inflow and outflow faces of the network. When the nonwetting phase is injected into the inflow face of the network in drainage process, the local capillary pressure increases in invaded face and decreases in the outlet face. Because the local wetting phase saturation is the least in invaded face and the wetting phase saturation is the most in the outlet face (derived from capillary pressure-saturation curve). Therefore, the created capillary force or pressure gradient acts as resisting force for the non-wetting and wetting fluid flow rates in drainage process through the anisotropic porous media in capillary non-equilibrium situations. When the wetting phase is injected into the inflow face of the network in imbibition process, the local capillary pressure decreases in invaded face and increases in the outlet face. Because, the local saturation of the wetting phase fluid is the most in invaded face and the local saturation of the wetting phase fluid is the least in outlet face of the network (derived from capillary pressure-saturation curve). Therefore, the created capillary force or pressure gradient acts as the assisting force for wetting and non-wetting fluid flow rates in imbibition process through an anisotropic porous medium in capillary nonequilibrium situation.

We have used the thermodynamics theory of non-equilibrium process to calculate two-phase flow rate through an anisotropic porous media in capillary non-equilibrium situation. It is assumed that the driving forces are the imposed macroscopic pressure gradient and the created capillary pressure gradient in two-phase flow through an anisotropic porous media for capillary nonequilibrium situation. The capillary pressure gradient is created by interactions between the fluids and the surface of the solid. The capillary pressure gradient throughout the network can be expressed as following:

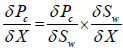   (10)

Using the thermodynamic theory of non-equilibrium process, we suggest the following relations for calculating the non-wetting and wetting flow rates in anisotropic porous media for capillary non-equilibrium situation:

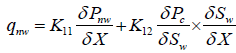   (11)

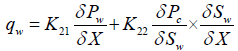   (12)

We substitute 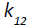and 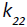instead of 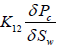and 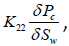respectively. We obtain the following relationships:

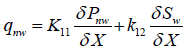   (13)

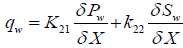   (14)

K11 and K21 are the effective permeabilities which are the second rank tensor in anisotropic porous media. The transport coefficients k12 and k22 are the second rank tensor in anisotropic porous media. They are the properties of the considered porous media. When the system reach to capillary equilibrium situation, second terms of equations 20 and 21 are eliminated.

Conclusion

Our main purpose of this study is the investigation of the ability of Darcy’s law for extension in two-phase flow for the sedimentary medium in the capillary non-equilibrium situations. The study has been accomplished using the correlated anisotropic network modeling. The main conclusions of this study are:

(1) In the sedimentary medium for the capillary non-equilibrium situations, relative permeability depends on the direction of the capillary force and cannot be expressed as a scalar quantity.

(2) In the sedimentary medium simulated as the anisotropic correlated network model and the capillary non-equilibrium situations, relative permeability of the non-wetting phase in the parallel direction to the bedding is greater than that in the perpendicular direction to the bedding. The reason of this difference is the distinct correlations between the throat radii in the parallel and perpendicular directions of the sedimentary medium.

(3) The effective permeability requires three directions to be described in the sedimentary medium for the capillary nonequilibrium situations. The new direction is the orientation of the capillary forces which are the driving force for cited situations.

(4) Darcy’s law cannot be extended in two-phase flow for the sedimentary medium in the capillary non-equilibrium situations.

(5) We have used the thermodynamics theory of non-equilibrium process to present the new relationships which calculate accurately wetting and non-wetting fluid flow rates with two driving forces through the anisotropic porous media for the capillary non-equilibrium situations.

References

1. Bear J (1972) Dynamics of fluid in porous media. New York: America Elsevier Publishing Co.
2. Bear J, Braester C, Menier P (1987) Effective and relative permeabilities of anisotropic porous media. Transport in Porous Media 2: 301-316.
3. Corey A, Rathjens C (1956) Effect of stratification on relative permeability. J. Pet. Tech 8: 358-360.
4. Kortekaas T. (1985) Water/oil displacement characteristics in cross bedded reservoir zones. Paper SPE 12112 presented at Annual Technical Conference and Exhibition, San Francisco.
5. Inverson WP, Dunn TL, Ajdari I (1996) Relative permeability anisotropy measurements in Tensleep sandstones. Paper SPE 35435 presented at 10th Symposium on Improved Oil Recovery, Tulsa.
6. Ajdari I (1995) Anisotropy of relative permeability within the Tensleep sandstone. Thesis (M.S.) in Petroleum Engineering: University of Wyoming.
7. Paterson L, Painter S, Zhang X, Pinczewski V (1996) Simulating residual saturation and relative permeability in heterogeneous formations. Paper SPE 36523 presented at the SPE Annual Technical Conference and Exhibition, Denver, Colorado.
8. Hewett TA (1986) Fractal distributions of reservoir heterogeneity and their influence on fluid transport. Paper SPE15836 presented at 16th Annual Technical Conference, New Orleans, Louisiana.
9. Sahimi M (1994) Long-rang correlated percolation and flow and transport in heterogeneous porous media. J Phys 4: 1263-1268.
10. Knackstedt MA, Sheppard AP, Sahimi M (2001) Pore network modeling of two-phase flow in porous rock: the effect of correlated heterogeneity. Advances in Water Resources 24: 257-277.
11. Knackstedt MA, Sheppard AP, Pinczewski WV (1998) Simulation of mercury porosimetry on correlated grids: evidence for extended correlated heterogeneity at the pore scale in rocks. Physical Review E 58: 6923-6926.
12. https://fraclab.saclay.inria.fr/.
13. Hassanizadeh SM, Gray WG (1993) Thermodynamic basis of capillary pressure in porous media. Water Resource Research 29: 3389-3405.
14. Hassanizadeh SM, Celia MA, Dahle HK (2002) Dynamic effects in the capillary pressure-saturation relationship and their impacts on unsaturated flow. Journal of Vadose Zone l: 38-57.
15. Joekar-Niasar V, Hassanizadeh SM, Dahle HK (2010) Non-equilibrium effects in capillary and interfacial area in two-phase flow: dynamic pore-network modeling. Journal Fluid Mechanics 655: 38-71.
16. Brooks RH, Corey AT (1964) Hydraulic properties of porous media. Hydraulic Paper 1964; Colorado State University 3: 24.
17. Li K (2004) Theoretical development of the Brooks-Corey capillary pressure model from fractal modeling of porous media. Paper SPE 89429 presented at fourteenth symposium on Improved Oil Recovery, Oklahoma.
18. Fatt I (1956) The network model of porous media: I. Capillary pressure characteristics. Pet Trans 207: 144-159.