Commentary

Game logic is a dynamic modal logic which models strategic two person games; it contains propositional dynamic logic (PDL) as a fragment. We propose in [1-4] an interpretation of game logic based on stochastic effectivity functions. This comment is a brief introduction to this logic and its interpretation, in particular we point out why we need to introduce a new formalism beyond stochastic Kripke models [5-10].

In his paper [11], van Benthem remarks “Game logics describe general games through powers of players for forcing outcomes", describing models for situations like general two person games of the kind already discussed by Zermelo [12] like markets of commodities, the analysis of arguments between a proponent and a critic of a claim, termination of distributed systems and many more. The general situation models that two players play against each other, each player working toward a winning situation. It is assumed that exactly one of the players will win the game, so draws are excluded. The players are considered to be equivalent, so that not one player dominates the other one.s In fact, we will assume that the actions of player 2 can be modelled by the actions of player 1 simply by interchanging their roles.

Modal logics

Let us first risk a quick glance at modal logics. Its formulas are supposed to model changes of states (so we live in a set of states, which are sometimes called worlds), they are given through this grammar.

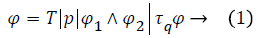
Here p is a primitive formula, which we assume to be given from the outside, q ∈[0,1] ∩Q is a numerical value, and τ is a game. Actually, modal logics are usually defined a bit more general with general actions rather than games in mind, and they offer negation as an operation [1]. This logic, however, is negation free, since we do not need it here, it has, apart from conjunction, a decorated modal operator, the decoration of which will be omitted in the non-probabilistic case. Intuitively, formula 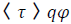is true in a state s if playing game τ in state s will result in a state in which formula φ holds with a probability greater than q. We assume that states change according to some probability laws, which may depend on the modal operator τ. An interpretation of this logic will have to record the effects of the modal operators on these probabilities.

Given a state and a game, each player has in this state certain possibilities to force an outcome when playing this game, i.e., a set of states from which the next state may be selected. We do not give, however, policies which help the players in arriving at decisions which next state or even which set of possible next states to select. The mechanisms for these decisions are assumed to be outside the realm of the game and can be found, e.g., in stochastic dynamic programming [8].

Games

Games in turn are given by this grammar

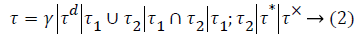
With γ∈Γ, the set of atomic games. This models a two person game, player 1 is called Angel, player 2 is referred to as Demon Angel plays against Demon. Games can be combined in different ways. If τ and τ′ are games, τ;τ′ is the sequential composition of τ and τ′, so that plays , τ first, than τ′. In game τ ∪ τ′, Angel decides whether τ or τ′ is to be played, then the chosen game is played; τ ∪ τ′ is called the angelic choice between τ and τ′. Similarly, in τ ∩ τ′ Demon decides whether τ or τ′ is to be played; accordingly, τ ∩ τ′ is the demonic choice between the games. In the game τ*, game τ is played repeatedly, until Angel decides to stop; it is not said in advance how many times the game is to be played, probably even not at all, but it has to stop at some time; this is called angelic iteration. Dually, Demon decides to stop for the game τ^×; this is called demonic iteration. Finally, the roles of Angel and Demon are interchanged in the game τ^d, so all decisions made by Demon are now being made by Angel, and vice versa.

Let's see how to interpret a game in the absence of probabilities. We assume the availability of a relation 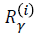which indicates that player i has a strategy for forcing a set A of outputs upon playing in state by s by 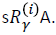Thus 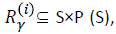the latter denoting the power set of state space S. It is desirable thats 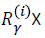and 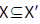together imply 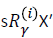for all states s. → (3)

We assume that the game is determined, i.e., that exactly one of the players has a winning strategy. Thus A⊆S is effective for player 1 in state s if and only if A\S is not effective for player 2 in that state. Consequently,

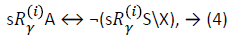
which in turn implies that we only have to cater for player 1. We will omit the superscript from the neighbourhood relation R_γ. In this way we associate with each game a map S→P (S) from the set S of states to its power set P (S), for convenience also called R_γ which in addition is upper closed, i.e., A∈R_γ(s), A⊆B implies B∈P(S). These maps are traditionally called effectivity functions. Clearly, a relation M⊆S×S yields such an effectivity function M• upon setting

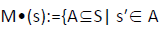for some s′ with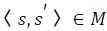

We will return to this point later on.

Towards an interpretation

From R_γ another map 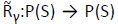is obtained upon setting 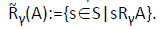Thus state s is an element of 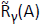if the first player has a strategy force the outcome A when playing γ in s. The algebraic operations on games can be taken care of through this family of maps, e.g., one sets recursively

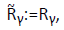if γ is atomic, i.e., if γ∈ Γ → (6)

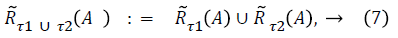
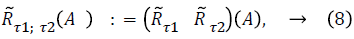
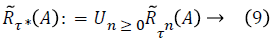
This refers only to player 1, player 2 is accommodated through 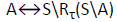by (4). The maps R̃_τ serve in Parikhs's original paper [10] as a basis for defining the semantics of game logic. It turns out to be convenient for the present paper, however, to use effectivity functions as maps to upper closed subsets.

Just to provide an example for this interpretation, assume that [[φ]] is the set of all states for which formula φ holds, then 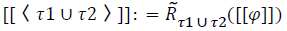will be the set of states in which φ holds after the angelic choice between games τ1 and τ2 has been made.

What about probabilities?

Having a look at the algebraic operations on the maps R̃_γ, one perceives that some common operations enter the model, viz., unions and compositions. Let us call Parikh's approach the nondeterministic interpretation. Constructing a probabilistic interpretation, the first attempt would be to mimic somehow the approach given above. Alas, this does not work, since it does not make too much sense to talk about the union of probabilities, say, as in (7). Consequently we have to modify this approach accordingly, guided by these considerations (with P_γ playing the probabilistic role of R_γ):

where the non-deterministic approach uses subsets of states, we will use subsets of probabilities on states. A∈R_γ(s) means non-deterministically that, playing in s, the player has a strategy to achieve a state in A. In the probabilistic transformation we will say that A∈P_γ(s) means that A is a set of probability measures yielding the distributions of the states upon playing γ in s. P_γ(s) should be upper closed, in accordance with (3) for its non-deterministic cousin. We deal with probabilities over general spaces, which require a measurable structure (technically, the state space S is equipped with a Boolean σ- algebra of subsets which are called measurable. This measurable structure induces a measurable structure on the space of all probabilities on S; first details can be found, e.g., in [5], an indepth discussion in [3,1.6, 4.1.2]). P_γ should behave decently with respect to this measurable structure.

We collect these properties and call the corresponding map P a stochastic effectivity function for game γ. It turns out that these functions have quite a number of interesting properties, algebraically [2] and with respect to modelling stochastic nondeterminism [7]. In this way, stochastic effectivity functions are used for interpreting game logics. Just to provide simple examples for the recursive approach, consider primitive games and angelic choice again. Recall that validity is decorated with a threshold value in the probabilistic case.

Game γ is primitive

Thus Angel has a strategy for achieving state s in φ upon playing primitive game γ with probability not smaller than q if all probabilities assigning a value not smaller than q to [[φ]] are feasible for P γ (s). This translates to

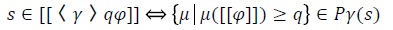
Angelic choice

We combine the probabilities for 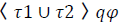from their constitutent parts, partitioning the probabilities accordingly, hence:

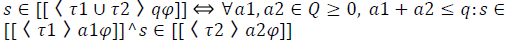
The other cases are delt with similarly

We have among others to cater for Demon, and we have to take care of the composition (8) as well as the in_nite iteration (9) of games. The latter part is technically quite involved, so the reader is referred to [4,5].

Special case: Kripke Models: Let us first note that Kripke models that are usually used for stochastically interpreting modal logics [3,6] are a special case. In a Kripke model, we assign for each action to each state a distribution over the set of states, indicating the probabilities for a state change after the action in that state. Using the construction indicated in Equ. (5), it can be shown that a Kripke model induces a family of stochastic effectivity functions which may be used for

This raises the question whether the extension to stochastic effectivity functions is really necessary. But it is: Kripke models are distributive, which means that interpreting a game model.

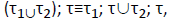
≡ indicating equality for each validity set. A little reflection shows, however, that this should not be the case in general. General stochastic effectivity functions do not observe that property, which means that the generalization pays off.

Special case: PDL: An important class of games is given by programs, which can be perceived as those games that are being played with one player only, with a similar informal semantic understanding. Programs are given by this grammar

with π taken from a set of primitive programs. The corresponding logic is usually called propositional dynamic logic, abbreviated as PDL. Thus programs can be combined through sequential composition and through the choice operator; we have also indefinite iteration of programs.

PDL is usually interpreted probabilistically through stochastic Kripke models [9]. It can luckily be shown that the Kripke interpretation coincides with the interpretation through the effectivity functions constructed above.

Conclusion

The stochastic interpretation of game logics requires adding stochastic electivity functions to the traditional tool kit. This extension is sketched here. Further work will include an algebraic study going beyond the work already done in [2], focussing in particular on monadic aspects. One would like to understand better, for example, the relationship of these functions to the Giry monad.

Acknowledgment

Some of the work was done while the author, now retired, held the Chair of Software Technology at the Technische Universitat Dortmund. It was funded in part by Deutsche Forschungsgemeinschaft, grant DO 263/12-1, Koalgebraische Eigenschaften stochastischer Relationen.

References

1. Blackburn P, Rijke M de, Venema Y (2001) Modal Logic. Number 53 in Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, Cambridge, Uk.
2. Doberkat EE (2014) Algebraic properties of stochastic e_ectivity functions. J Logic and Algebraic Progr 83: 339-358.
3. Doberkat EE (2015) Special Topics in Mathematics for Computer Science: Sets, Categories, Topologies, Measures. Springer International Publishing Switzerland, Cham, Heidelberg, New York, Dordrecht, London, December.
4. Doberkat EE (2017) A stochastic interpretation of game logic. J Logic and Algebraic Progr 88: 64-98.
5. Doberkat EE (2017) Using coalgebras and the Giry monad for interpreting game logics-a tutorial. Frontiers of Computer Science 11: 948-970.
6. Doberkat EE, Kurz A (2011) editors. Special Issue on Coalgebraic Logic. Math Struct Comp Sci 21: 2.
7. Doberkat EE, Terraf PS (2017) Stochastic nondeterminism and effectivity functions. J Logic and Computation 27: 357-394.
8. Hinderer K (1970) Foundations of Non-stationary Dynamic Programming with Discrete Time Parameter. Number 33 in Lect. Notes Op Res Math Syst Springer-Verlag, Berlin.
9. Kozen D (1985) A probabilistic PDL. J Comp Syst Sci 30: 162-178.
10. Parikh R (1985) The logic of games and its applications. In M Karpinski and J van Leeuwen Editors. Topics in the Theory of Computation 24: 111-140.
11. van Benthem J (2003) Logic games are complete for game logics. Studia Logica 75: 183-203.
12. Zermelo E (1913) Uber eine Anwendung der Mengenlehre auf die Theorie des Schachspiels. In EW Hobson and AEH Love, editors Proc. Fifth Int. Congress of Mathematicians, Cambridge, UK Cambridge University Press 2.